Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn, intersecting AC in L and AD produced in El. Prove that EL= 2BL
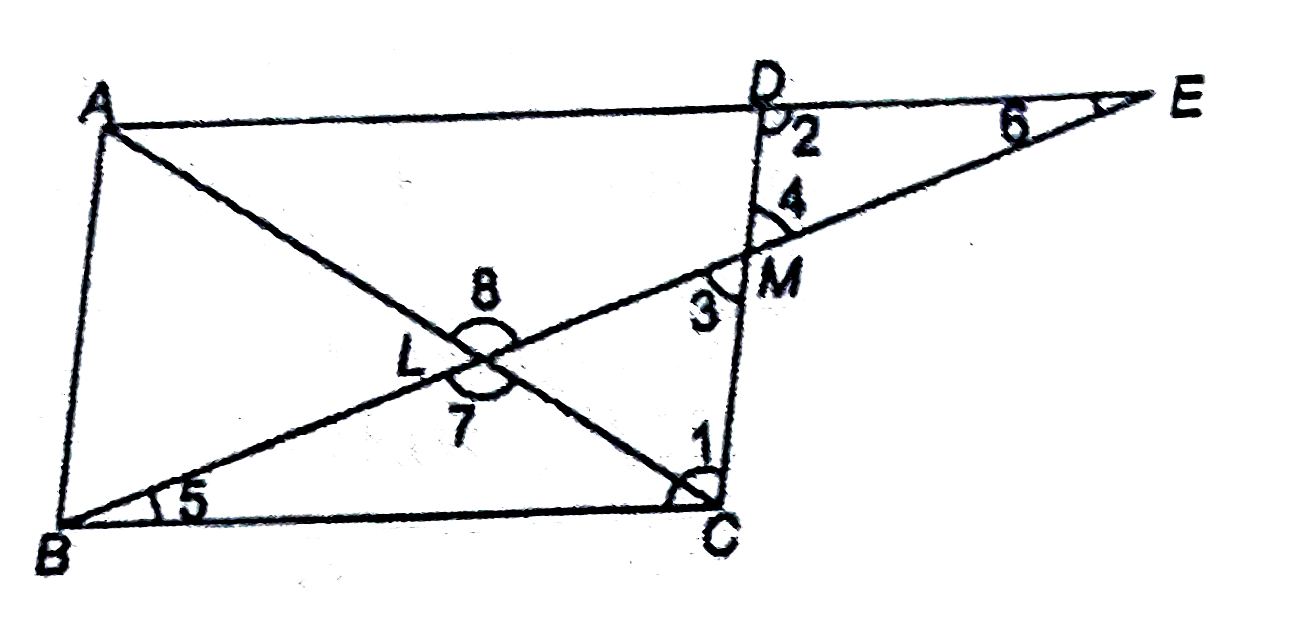
In triangles BMC and DME,

△BMM≅△EMD ( ASA criterion)
BC=ED (corresponding parts of congruent triangle)….(1)
BC=AD (opposite sides of a prallelogram) ..(2)
Adding (1) and (2) , we get
2BC=DE+AD⇒2BC=AE
⇒BCAE=12 ....(3)
Now in △BCLand△EAL
∠5=∠6 (alternate ∠s as BC||AE)
∠7=∠8 ( vertically opposite angles)
△BCL~△EAL (AA corollary)
BCEA=BLEL (corresponding sides of similar triangles are proportional) ...(4)
12=BLEL [ from (3) and (4) ]
EL=2BL Hence proved.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar14videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Exercise 6a23videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions5videos
STATISTICS
- BOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions5videos
VOLUME AND SURFACE AREA OF SOLIDS
Similar Questions
Through the mid-point M of the side CD of a parallelogram ABCD , the line BM is drawn intersecting AC at LandAD produced at E . Prove that EL=2BL.
View SolutionP is the mid-point of the side CD of a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.
View SolutionP is the mid-point of side AB of parallelogram ABCD. A line drawn from B parallel to PD meets CD at Q and AD produce at R. Prove that :
(i) AR = 2BC (ii) BR= 2BQView SolutionThrough the vertex D of a parallelogram ABCD, a line is drawn to intersect the sides BA and BC produced at E and F respectively. Prove that DAAE=FBBE=FCCD
View SolutionP is the mid-point of side AB of a parallelogram ABCD . A Line through B parallel to PD meets DC at Q and AD produced at R . Prove that (i) AR=2BC (ii) BR=2BQ.
View Solution
The mid-point of side CD of parallelogram ABCD is 'm' in the given figure what is the ratio ON : OB?View SolutionP is the mid-point of the side AD of the parallelo- gram ABCD. The line BP meets the diagonal AC in Q and the line CD in R. Then RQ:QB is equal to
View SolutionIn a parallelogram ABCD, the bisector of ∠A bisects the line Bcat point X. Prove that AD = 2AB.
View SolutionThe diagonals of a parallelogram ABCD intersect at O.A line through O intersects AB at X and DC at Y. Prove that OX=OY.
View SolutionABCD is a parallelogram. The circle through A, B and C intersect CD (produced ifnecessary) at E. Prove that AE = AD.
View Solution

