To evaluate limx→a[f(x)], we must analyse the f(x) in right hand neighbourhood as well as in left hand neighbourhood of x=a. E.g. In case of continuous function, we may come across followign cases.
![To evaluate lim(xtoa)[f(x)], we must analyse the f(x) in right hand neighbourhood as well as in left hand neighbourhood of x=a. E.g. In case of continuous function, we may come across followign cases. If f(a) is an integer, the limit will exist in Case III and Case IV but not in Case I and Case II. If f(a) is not an integer, the limit exists in all the cases. ltbgt If f'(1)=-3 and lim(xto1)[f(x)-1/2] does not exist, (where [.] denotes the greatest integer function), then](https://d10lpgp6xz60nq.cloudfront.net/physics_images/ARH_AAG_DIF_CAL_C05_SLV_114_Q01.png)
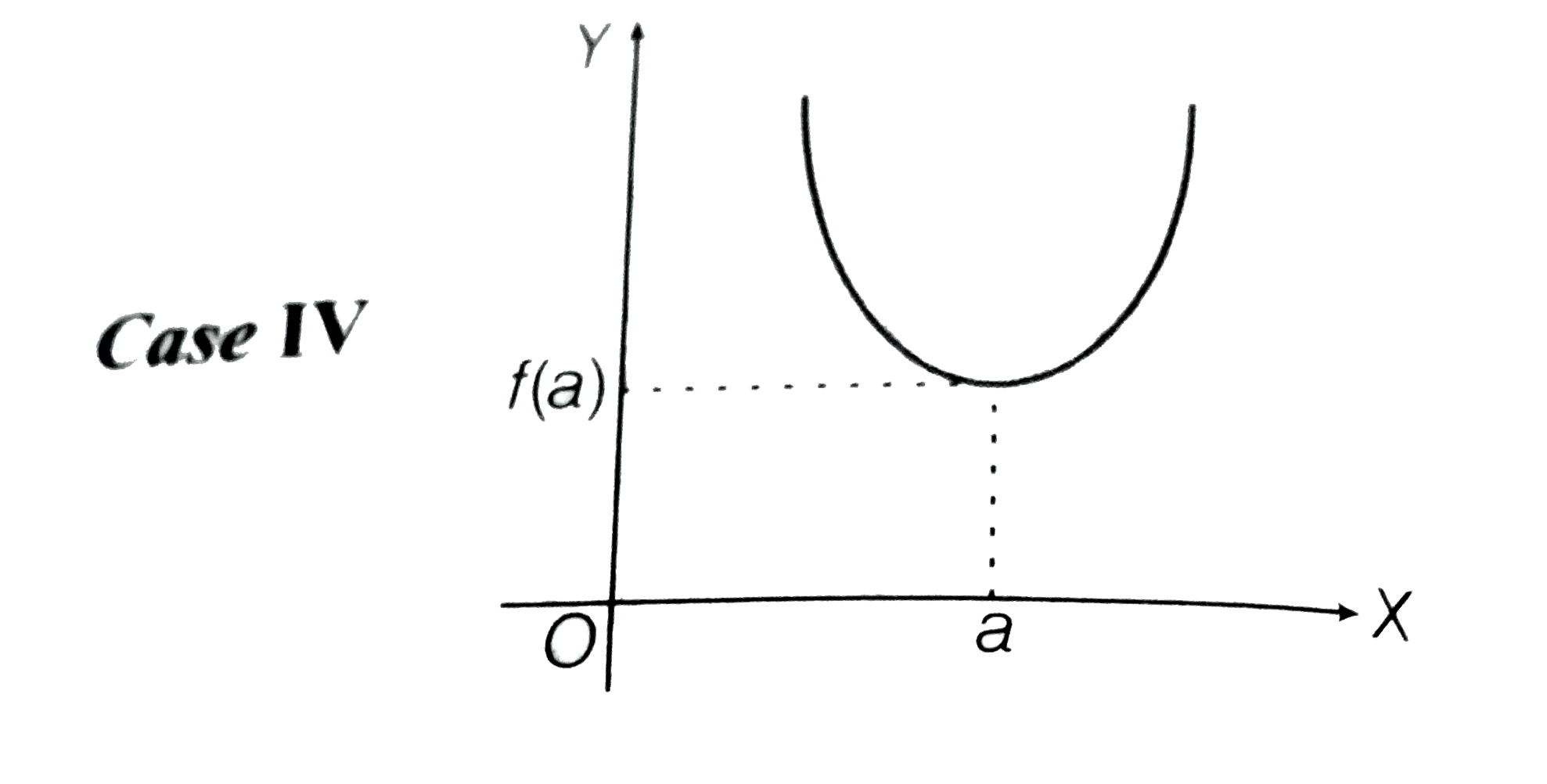
Iff(a) is an integer, the limit will exist in Case III and Case IV but not in Case I and Case II. If f(a) is not an integer, the limit exists in all the cases. ltbgt If f'(1)=−3 and limx→1[f(x)−12] does not exist, (where [.] denotes the greatest integer function), then Solution in Punjabi
The correct Answer is:A
Step by step video & image solution for To evaluate lim_(xtoa)[f(x)], we must analyse the f(x) in right hand neighbourhood as well as in left hand neighbourhood of x=a. E.g. In case of continuous function, we may come across followign cases. If f(a) is an integer, the limit will exist in Case III and Case IV but not in Case I and Case II. If f(a) is not an integer, the limit exists in all the cases. ltbgt If f'(1)=-3 and lim_(xto1)[f(x)-1/2] does not exist, (where [.] denotes the greatest integer function), then by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - Exercise (Single Option Correct Type Questions)38videos
LIMITS
- BOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - Exercise (More Than One Correct Option Type Questions)15videos
LIMITS
- BOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - Exercise For Session 65videos
LIMITS
- BOOK - ARIHANT MATHSCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)8videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - ARIHANT MATHSCHAPTER - LOGARITHM AND THEIR PROPERTIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)4videos
LOGARITHM AND THEIR PROPERTIES
Similar Questions
limx→0sin(πcos2(tan(sinx)))x2 is equal to
01:37View SolutionIf limx→∞4x(π4−tan−1(x+1x+2))=y2+4y+5 then y can be equal to
06:07View SolutionThe value o limx→∞(1n3)([12x+12]+[22x+22]+…..+[n2x+n2]) is where [.] denotes the greatest integer function.
02:11View SolutionIf α=3sin−1(611andβ=3cos−1(49), where the inverse trigonometric functions take only the principal values, then the correct options (s) is (are)
01:31View SolutionIn Which quadrant Point (−2,−3) will be lie.
02:45View SolutionHow many lines of symmetry does the above figure have ?
02:17View SolutionWhich of the following are correct chain isomers of butane ? (i)
05:41View SolutionDetermine the point of symmetry of a regular hexagon.
02:10View SolutionDtermine the images of the following figure about the given line :
02:17View SolutionMatch the following Column A to Column B
 02:10View Solution
02:10View SolutionMatch the following Column A to Column B
 04:23View Solution
04:23View SolutionMatch the following Column A to Column B
 01:13View Solution
01:13View SolutionThe inequation represented by the graph given below is :
04:42View SolutionThe inequation that best describes the graph given below is _________
05:08View SolutionThe inequation that best describes the following graph is _________
03:46View Solution

