To find the area of △ABC, note that the lengths of the sides of △ABC form (3-4-5) Pythagorean triple, where AC=4. Hence, Find the area of △ABC.
The correct Answer is:6
To find the area of triangle ABC, we can follow these steps:
Step 1: Identify the sides of the triangle
Given that triangle ABC forms a Pythagorean triplet (3-4-5) and that AC = 4, we can identify the sides of the triangle:
- AC = 4 (one of the perpendicular sides)
- BC = 3 (the other perpendicular side)
- AB = 5 (the hypotenuse)
Step 2: Understand the triangle configuration
Since AC and BC are the two perpendicular sides, we can visualize triangle ABC as a right-angled triangle with:
- AC as the height
- BC as the base
Step 3: Use the area formula for a triangle
The area A of a triangle can be calculated using the formula:
A=12×base×height
In our case:
- Base = BC = 3
- Height = AC = 4
Step 4: Substitute the values into the formula
Now substituting the values into the area formula:
A=12×3×4
Step 5: Calculate the area
Calculating the above expression:
A=12×12=6
Conclusion
Thus, the area of triangle ABC is 6 square units.
---
Given that triangle ABC forms a Pythagorean triplet (3-4-5) and that AC = 4, we can identify the sides of the triangle:
- AC = 4 (one of the perpendicular sides)
- BC = 3 (the other perpendicular side)
- AB = 5 (the hypotenuse)
Since AC and BC are the two perpendicular sides, we can visualize triangle ABC as a right-angled triangle with:
- AC as the height
- BC as the base
The area A of a triangle can be calculated using the formula:
A=12×base×height
In our case:
- Base = BC = 3
- Height = AC = 4
Now substituting the values into the area formula:
A=12×3×4
Calculating the above expression:
A=12×12=6
Thus, the area of triangle ABC is 6 square units.
Topper's Solved these Questions
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - Multiple Choice
99 Videos
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - Grib-In
32 Videos
- ADDITIONAL TOPICS IN MATH BOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATH EXERCISE - PRACTICE TEST
24 Videos
- COMPLEX NUMBERSBOOK - ENGLISH SATCHAPTER - COMPLEX NUMBERSEXERCISE - EXERCISE
6 Videos
Similar Questions
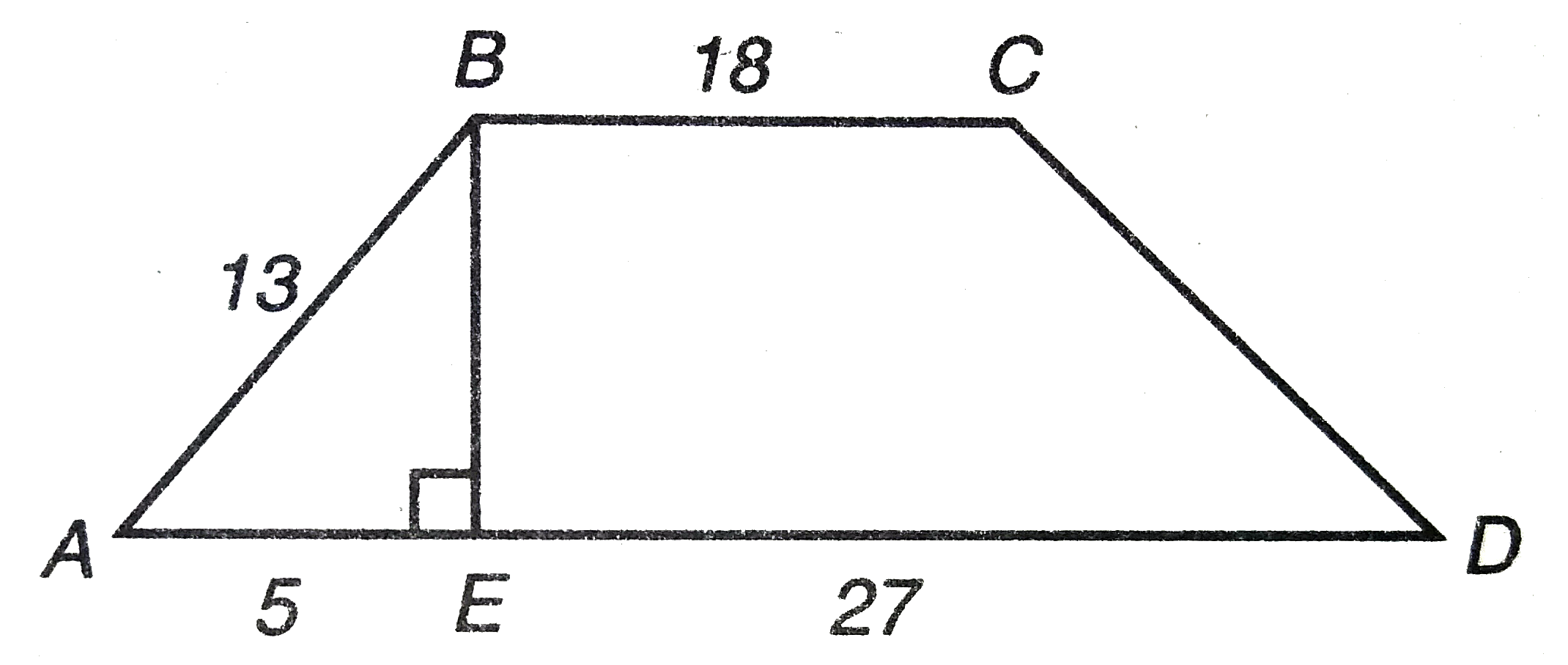
To find the area of trapezoid ABCD, use the fact that the lengths of the sides of right triangle AEB form a (5-12-13) Pythagorean triple, where height BE=12. The length of lower base AD=AE+ED=5+5+27=32
View SolutionThe lengths of the sides of a triangle are in the ratio 4 : 5 : 3 and its perimeter is 96 cm. Find its area.
View Solution
Knowledge Check
Find the area of an equilateral triangle with a side length of 12
A6√3B18√3C36√3D72√3The area of △ABC,=24√3, side a=6, annd side b=16. the value of ∠C is
A30∘B30∘ or 150∘C60∘D60∘ or 120∘
The lengths of the sides of a triangle are in the ratio 4:5:3 and its perimeter is 96 cm. Find its area.
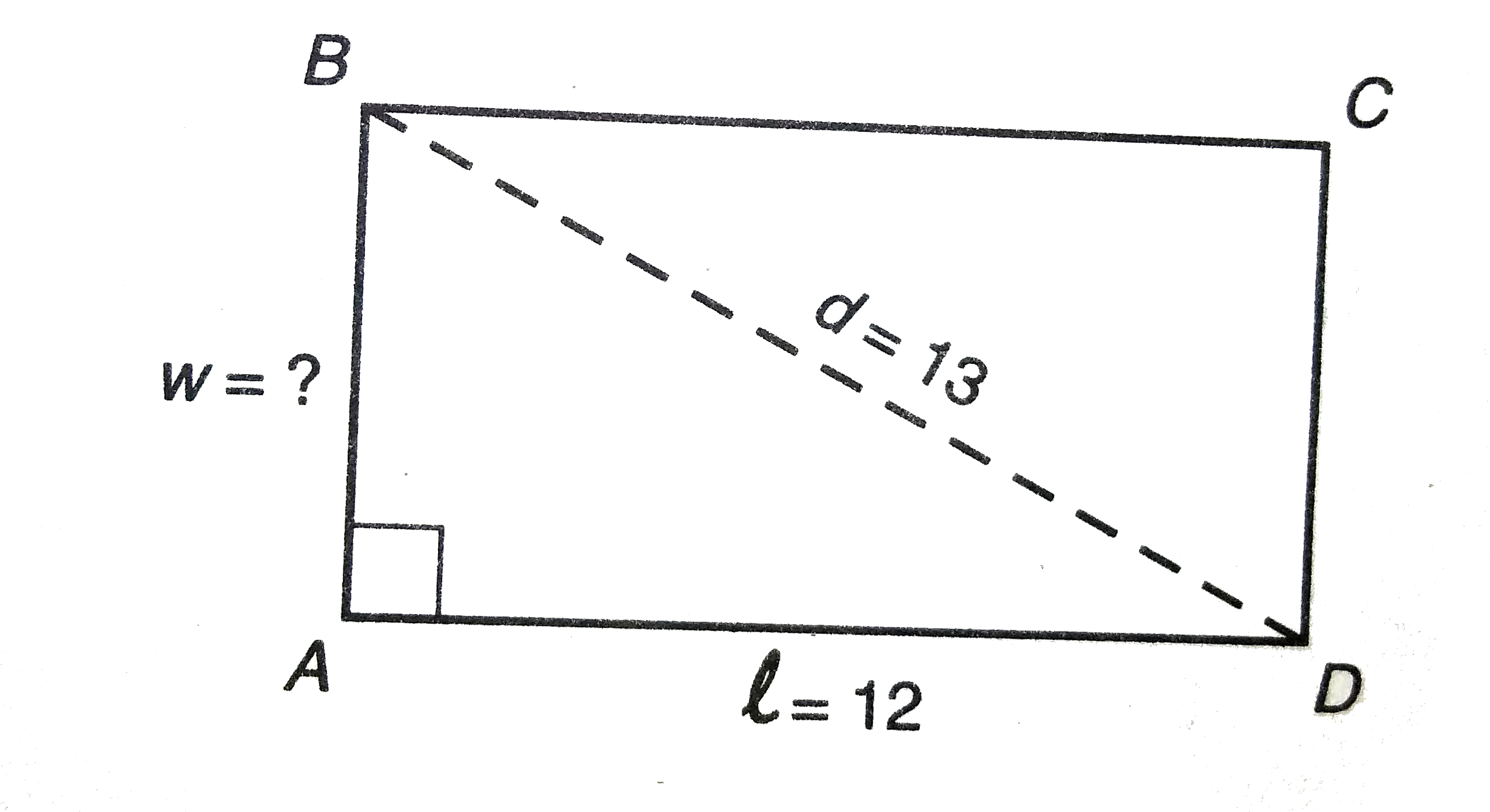
View SolutionTo find the area of rectangle ABCD, note that the diagonal form a (5−12−13) right triangle so the width of the rectangle is 5. Hence,Find area of triangle.:
View SolutionThe length of the sides of a triangle are in the ratio 3:4:5. Find the area of the triangle if its perimeter is 144 cm.
View SolutionFind the area of a rectangle whose length is 5.5 m and breadth is 3.4 m.
View SolutionFind the area of a rectangle of length 4 m and breadth 120 cm.
View SolutionFind the length of the side of a square whose area is 441m2.
View Solution
