To the circle x2+y2=4 two tangents are drawn from P(−4,0), which touch the circle at T1, and T2 and a rhombus PT1P'T2 is completed. Circumcentre of the triangle PT1T2 is at
(−2,0)
(2,0)
(√3/2,0)
none of these
The correct Answer is:1
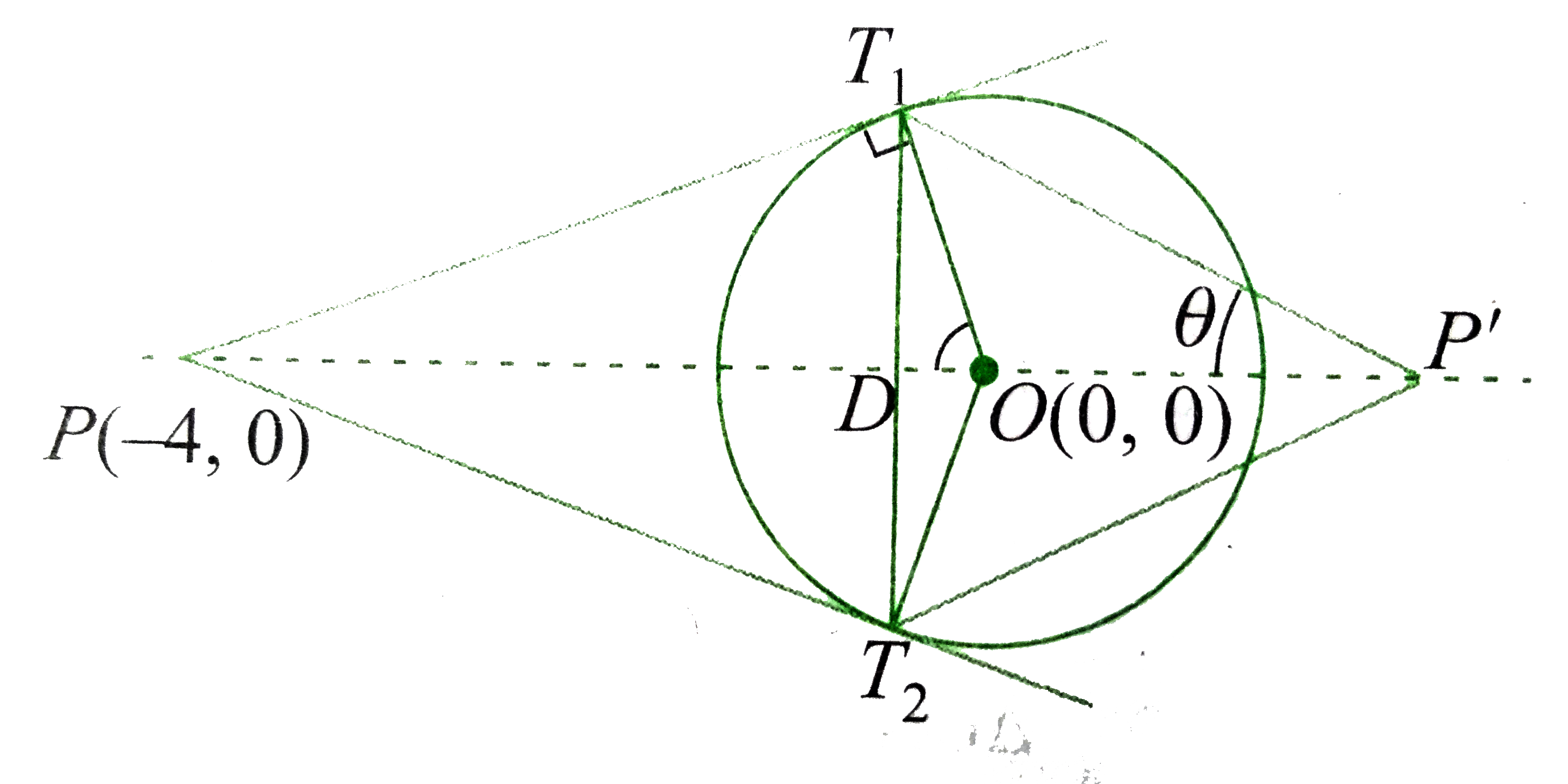
PT2=PT1=√(−4)2+o2−4=2√3
The circumcenter of triagnel PT1T2is the mdipoint of PO as
∠PT1O=∠PT2O=90∘
so, (−4+02,0+02)≡(−2,0)
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE
7 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - NUMERICAL VALUE TYPE
21 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)
3 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
To the circle x2+y2=4 two tangents are drawn from P(−4,0), which touch the circle at T1, and T2 and a rhombus PT1P'T2 is completed. Circumcentre of the triangle PT1T2 is at
View SolutionTo the circle x2+y2=4, two tangents are drawn from P(−4,0), which touch the circle at T1 and T2 . A rhomus PT1P'T2 s completed.
If P is taken to be at (h,0) such that P' lies on the circle, the area of the rhombus is
View Solution
Knowledge Check
To the circle x2+y2=4, two tangents are drawn from P(−4,0), which touch the circle at T1 and T2 . A rhomus PT1P'T2 s completed.
If P is taken to be at (h,0) such that P' lies on the circle, the area of the rhombus isA6√3B2√3C3√3Dnone of theseTangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B the equation of the circumcircle of △PAB is
Ax2+y2÷4x−6y+19=0Bx2+y2−4x−10y+19=0Cx2+y2−2x+6y−29=0Dx2+y2−6x−4y+19=0Tangents drawn from the point P (1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is
Ax2+y2+4x−6y+19=0Bx2+y2−4x−10y+19=0Cx2+y2−2x+6y−20Dx2+y2−6x−4y+19=0
Tangents PT1,andPT2, are drawn from a point P to the circle x2+y2=a2. If the point P line Px+qy+r=0, then the locus of the centre of circumcircle of the triangle PT1T2 is
View SolutionTangents PT1,andPT2, are drawn from a point P to the circle x2+y2=a2. If the point P lies on the line Px+qy+r=0, then the locus of the centre of circumcircle of the triangle PT1T2 is
View SolutionTangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is:
View SolutionTangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is:
View SolutionTangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is:
View Solution
