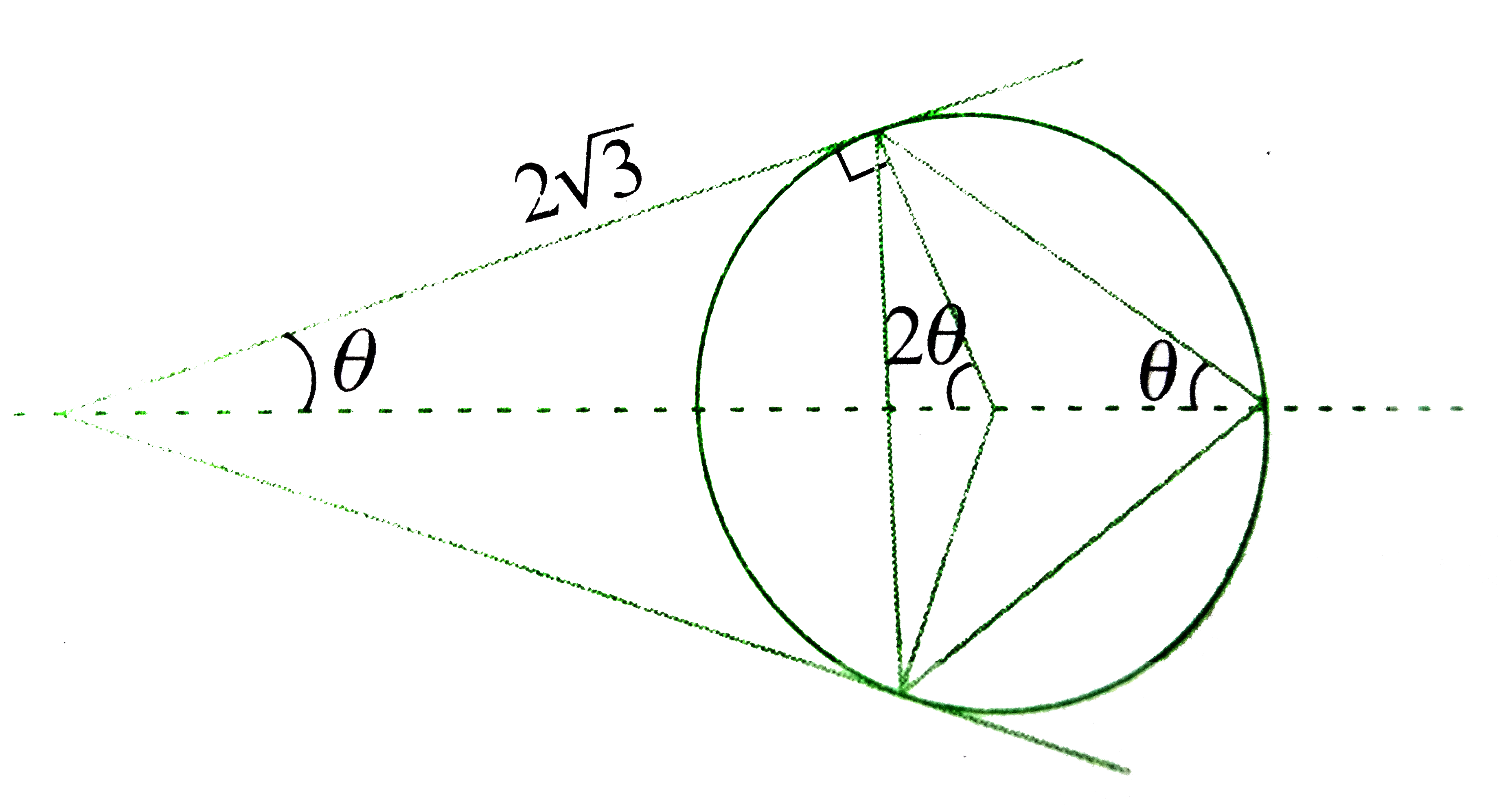
To the circle x2+y2=4, two tangents are drawn from P(−4,0), which touch the circle at T1 and T2 . A rhomus PT1P'T2 s completed.
If P is taken to be at (h,0) such that P' lies on the circle, the area of the rhombus is
6√3
2√3
3√3
none of these
The correct Answer is:1
Let P' be a point on the circle. Then,
3θ=π2
or θ=π6
Area of rhombus =(2√3)(2√3)sin.π3=6√3
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - NUMERICAL VALUE TYPE21videos
CIRCLE
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - ARCHIVES (JEE MAIN)1videos
CIRCLE
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)3videos
CIRCLE
- BOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix4videos
BINOMIAL THEOREM
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
Similar Questions
To the circle x2+y2=4 two tangents are drawn from P(−4,0), which touch the circle at T1, and T2 and a rhombus PT1P'T2 is completed. Circumcentre of the triangle PT1T2 is at
View SolutionTangents drawn from (2,0) to the circle x2+y2=1 touch the circle at AandB Then.
View SolutionFrom a point P on the normal y=x+c of the circle x2+y2−2x−4y+5−λ2−0, two tangents are drawn to the same circle touching it at point BandC . If the area of quadrilateral OBPC (where O is the center of the circle) is 36 sq. units, find the possible values of λ. It is given that point P is at distance |λ|(√2−1) from the circle.
View SolutionTwo tangents to the circle x2+y2=4 at the points A and B meet at P(−4,0), The area of the quadrilateral PAOB, where O is the origin, is
View SolutionLet T1,T2 and be two tangents drawn from (-2, 0) onto the circle C:x2+y2=1. Determine the circles touching C and having T1,T2 as their pair of tangents. Further, find the equations of all possible common tangents to these circles when taken two at a time
View SolutionP is a variable point on the line L=0 . Tangents are drawn to the circles x2+y2=4 from P to touch it at Q and R. The parallelogram PQSR is completed.
If P≡(3,4), then the coordinates of S areView SolutionTangents PT1,andPT2, are drawn from a point P to the circle x2+y2=a2. If the point P lies on the line Px+qy+r=0, then the locus of the centre of circumcircle of the triangle PT1T2 is
View SolutionP is a variable point on the line L=0 . Tangents are drawn to the circles x2+y2=4 from P to touch it at Q and R. The parallelogram PQSR is completed.
If P≡(6,8), then the area of ΔQRS isView SolutionP is a variable point of the line L = 0. Tangents are drawn to the circle x2+y2=4 from P to touch it at Q and R. The parallelogram PQSR is completed. If L=2x+y−6=0, then the locus of circumcetre of △PQR is -
View SolutionThe line 2x - y + 1 = 0 is tangent to the circle at the point (2,5) and the centre of the circles lies on x-2y = 4. The radius of the circle is :
View Solution

