True (T) or false (F)
If one member of a pythagorean triplet is 2m, then the other two members are
m,m2+1
m2+1,m2−1
m2,m2−1
m2,m+1
The correct Answer is:B
To determine whether the statement is true or false, we need to analyze the concept of Pythagorean triplets. A Pythagorean triplet consists of three positive integers a, b, and c such that they satisfy the equation:
a2+b2=c2
where c is the hypotenuse (the longest side) of a right triangle, and a and b are the other two sides.
Step 1: Identify the given member
We are given that one member of the Pythagorean triplet is 2m.
Step 2: Set up the Pythagorean theorem
Let’s denote the other two members of the triplet as a and b. According to the Pythagorean theorem, we can express this as:
(2m)2+a2=b2
Step 3: Substitute and simplify
Substituting 2m into the equation gives us:
4m2+a2=b2
Step 4: Rearranging the equation
We can rearrange this equation to find a relationship between a and b:
b2−a2=4m2
Step 5: Factor the difference of squares
The left side can be factored using the difference of squares:
(b−a)(b+a)=4m2
Step 6: Determine possible integer values
To satisfy this equation, b−a and b+a must be factors of 4m2.
Step 7: Find specific values
Assuming b−a=2m and b+a=2m, we can solve these equations:
1. b−a=2m
2. b+a=2m
Adding these two equations:
2b=4m⟹b=2m
Subtracting the first from the second:
2a=0⟹a=0
This means that b cannot be equal to 2m if we are looking for positive integers.
Conclusion
Since we cannot find two positive integers a and b such that one of the triplet members is 2m while satisfying the Pythagorean theorem, the statement is False (F).
We are given that one member of the Pythagorean triplet is 2m.
Let’s denote the other two members of the triplet as a and b. According to the Pythagorean theorem, we can express this as:
Substituting 2m into the equation gives us:
We can rearrange this equation to find a relationship between a and b:
The left side can be factored using the difference of squares:
To satisfy this equation, b−a and b+a must be factors of 4m2.
Assuming b−a=2m and b+a=2m, we can solve these equations:
2. b+a=2m
Since we cannot find two positive integers a and b such that one of the triplet members is 2m while satisfying the Pythagorean theorem, the statement is False (F).
Topper's Solved these Questions
- SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTBOOK - NCERT EXEMPLARCHAPTER - SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTEXERCISE - Exercise (Fill in the blanks to make the statements true.)
24 Videos
- SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTBOOK - NCERT EXEMPLARCHAPTER - SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTEXERCISE - Exercise (state whether the statements are true (T) or false (F))
38 Videos
- SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTBOOK - NCERT EXEMPLARCHAPTER - SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTEXERCISE - Think and Discuss
16 Videos
- RATIONAL NUMBERS BOOK - NCERT EXEMPLARCHAPTER - RATIONAL NUMBERS EXERCISE - Think and Discuss
1 Videos
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - THINK AND DISCUSS
2 Videos
Similar Questions
True (T) or false (F)
The top view of
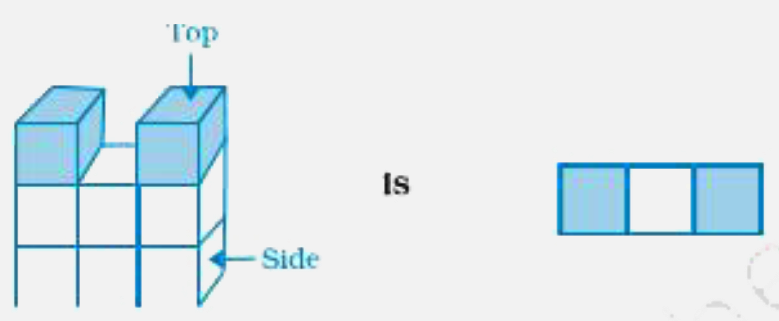
View SolutionState true (T) or false (F).
View SolutionFind a Pythagorean triplet in which one member is 12.
View SolutionAll numbers of a pythagorean triplet are odd. True or false.
View SolutionWrite two Pythagorean triplets each having one of the numbers as 5.
View Solutionpythagorean triplets in which one number is 12.
View SolutionWrite a Pythagorean triplet if one number is 14.
View Solutionwrite a Pythagorean triplet whose one member is (I)14 (ii) 16
View SolutionWrite a Pythagorean triplet whose smallest member is 8.
View SolutionWrite the Pythagorean triplet whose one of the numbers is 4.
View Solution
