Two circles are drawn inside a big circle with diameters23rd and13rd of the diameter of the big circle as shown in Fig.18. Find the area of the shaded portion, if the length of the diameter of the circle is 18 cm.
To find the area of the shaded portion in the given problem, we will follow these steps:
Step 1: Find the diameter of the big circle
The diameter of the big circle is given as 18 cm.
Step 2: Calculate the diameters of the two smaller circles
- Diameter of the first circle: This is 23 of the diameter of the big circle.
Diameter of first circle=23×18=12 cm
- Diameter of the second circle: This is 13 of the diameter of the big circle.
Diameter of second circle=13×18=6 cm
Step 3: Calculate the radius of each circle
- Radius of the big circle:
R=182=9 cm
- Radius of the first circle:
r1=122=6 cm
- Radius of the second circle:
r2=62=3 cm
Step 4: Calculate the area of each circle
- Area of the big circle:
Areabig=πR2=π(92)=81π cm2
- Area of the first circle:
Areafirst=πr21=π(62)=36π cm2
- Area of the second circle:
Areasecond=πr22=π(32)=9π cm2
Step 5: Calculate the area of the shaded portion
The area of the shaded portion can be calculated by subtracting the areas of the two smaller circles from the area of the big circle:
Areashaded=Areabig−Areafirst−Areasecond
Areashaded=81π−36π−9π=36π cm2
Final Answer
The area of the shaded portion is 36π cm2.
---
The diameter of the big circle is given as 18 cm.
- Diameter of the first circle: This is 23 of the diameter of the big circle.
Diameter of first circle=23×18=12 cm
Diameter of second circle=13×18=6 cm
- Radius of the big circle:
R=182=9 cm
r1=122=6 cm
r2=62=3 cm
- Area of the big circle:
Areabig=πR2=π(92)=81π cm2
Areafirst=πr21=π(62)=36π cm2
Areasecond=πr22=π(32)=9π cm2
The area of the shaded portion can be calculated by subtracting the areas of the two smaller circles from the area of the big circle:
Areashaded=Areabig−Areafirst−Areasecond
Areashaded=81π−36π−9π=36π cm2
The area of the shaded portion is 36π cm2.
Topper's Solved these Questions
Similar Questions
In the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
View SolutionThe diameter of a circle is 9 cm, find its radius.
View SolutionThe diameter of a circle is 14 cm, find its radius.
View SolutionThe diameter of a circle is 28 cm. Find its :
area
View SolutionIn figure , AB is a diameter of the circle, AC = 6cm and BC = 8cm . Find the area of the shaded region . (use π=3.14)

View SolutionCalculate the area of the shaded region, if the diameter of the semi-circle is equal to 14 cm.
(Take π=227)
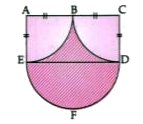
View SolutionABCP is a quadrant of a circle of radius 14 cm. with AC as diameter, a semicircle is drawn. Find the area of the shaded portion
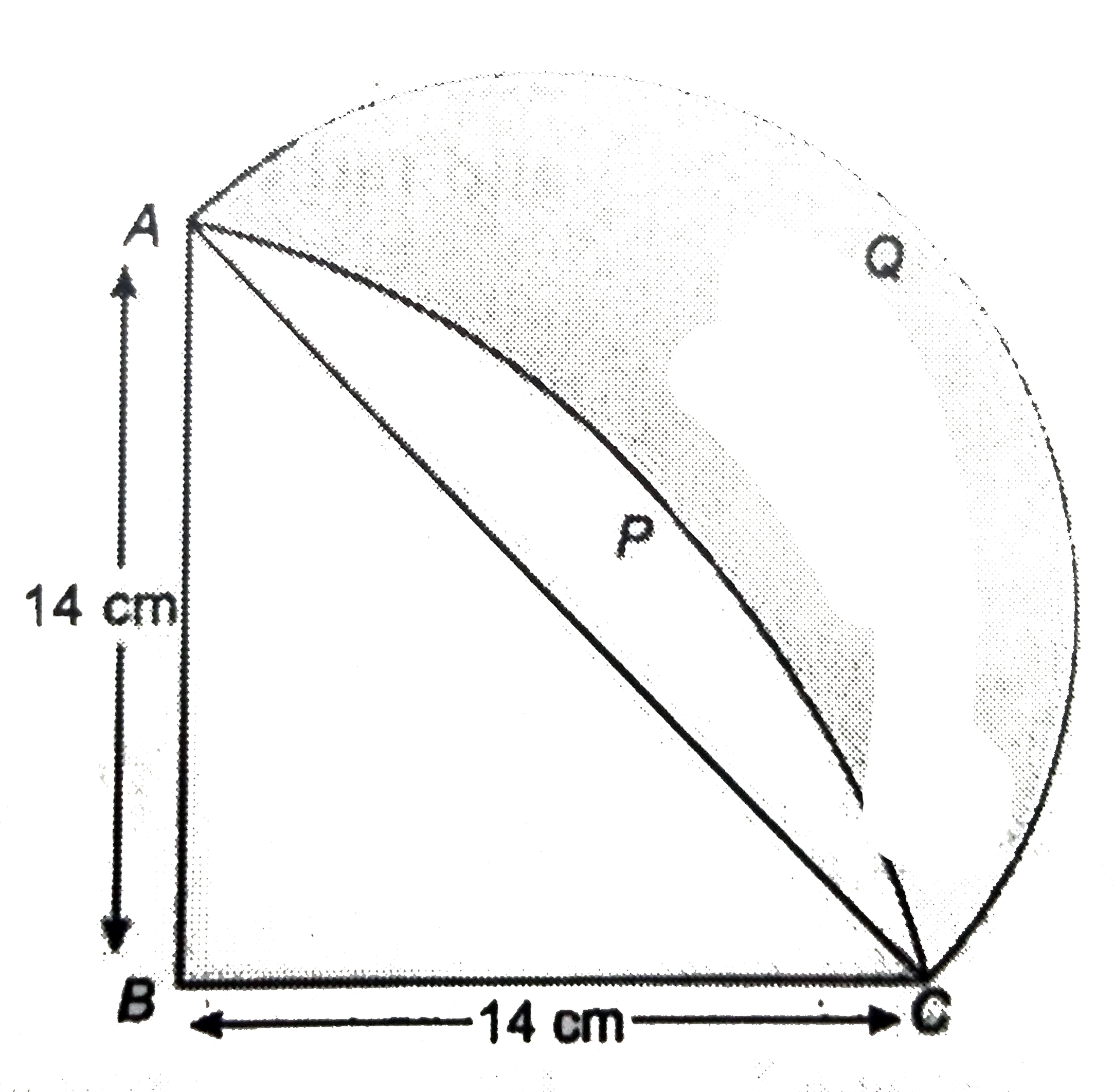
View SolutionThe diameter of two circles are 32 cm and 24 cm. Find the radius of the circle having its area equal to sum of the areas of the two given circle.
View SolutionABCP is a quadrant of a circle of radius 14 cm. With AC as diameter, a semi-circle is drawn. Find the area of the shaded portion.
View SolutionFind the area of a circle of diameter 7 cm.
View Solution