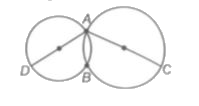
Two circles intersect at two points A and B. If AD and AC are diameters of the circles, then which of the following steps is INCORRECT in order to prove that B lies on the line segment DC?
(P) Join AB.
(Q) and (Angle in semicircle)
(R )
(S) DBC is a straight line segment. Hence B lies on the line segment DC.
P
Q
R
S
The correct Answer is:C
(R ) is incorrect. The correct step should be , for DBC to be a straight line segment.
Topper's Solved these Questions
- CIRCLES BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - CIRCLES EXERCISE - Achievers Section (HOTS)
3 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - Achievers Section (HOTS)
2 Videos
- CLASS 9 SAMPLE PAPER FINAL 4BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - CLASS 9 SAMPLE PAPER FINAL 4EXERCISE - MATHEMATICS
10 Videos
Similar Questions
Two circles intersect at two points A and B . AD and AC are diameters to the two circles .Prove that B lies on the line segment DC.
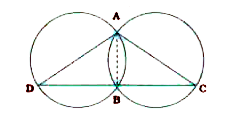
View SolutionTwo circles intersect at two points A and B. AD and AC are diameters to the two circles (see Fig.10.34). Prove that B lies on the line segment DC.
View Solution
Knowledge Check
If point P(4,2) lies on the line segment joining the points A(2,1) and B(8,4) then
AAP = PBBPB12PBCAP=12PBDAP=13PBIf the point P(2,1) lies on the line segment joining points A (4,2) and B (8,4) then :
AAP=13ABBAP = PBCPB=13ABDAP=12AB
In the figure, two circles intersect each other at points A and B. AP and AQ are the diameters of these circles. Prove that PBQ is a straight line.

View SolutionIf point P(4,2) lies on the line segment joining the points A(2,1) and B(8,4) then :
View SolutionTwo equal circles intersect in P and Q . A straight line through P meets the circles in A and B . Prove that QA=QB.
View SolutionThe line segment joining A(-2, 9) and B(6, 3) is a diameter of a circle with centre C. Find the coordinates of C.
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
View SolutionThe point P(-4,2) lies on the line segment joining the points A(-4,6) and B (-4,-6).
View Solution
