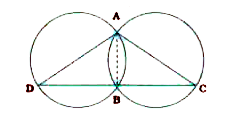
Two circles intersect at two points A and B. AD and AC are diameters to the two circles (see Fig.10.34). Prove that B lies on the line segment DC.
In∠ABD
∠ABD=900
In∠ABC
∠ABC=900
∠ABD+∠ABC=1800
DB||BC
B lies on line DC.
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - CIRCLESEXERCISE - Exercise 10.33videos
CIRCLES
- BOOK - NCERTCHAPTER - CIRCLESEXERCISE - Exercise 10.46videos
CIRCLES
- BOOK - NCERTCHAPTER - CIRCLESEXERCISE - Exercise 10.12videos
CIRCLES
- BOOK - NCERTCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE 9.11videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NCERTCHAPTER - CONSTRUCTIONSEXERCISE - EXERCISE 11.25videos
CONSTRUCTIONS
Similar Questions
Two circles intersect at two points A and B . AD and AC are diameters to the two circles .Prove that B lies on the line segment DC.
 View Solution
View SolutionIn the figure, two circles intersect each other at points A and B. AP and AQ are the diameters of these circles. Prove that PBQ is a straight line.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two circles with centres A and B of radii 3 cm and 4 cm respectively intersect at two points C and D, such that AC and BC are tangents to the two circle. Find the length of the common chord CD.
A4.2 cmB8.4 cmC2.4 cmD4.8 cm - Question 2 - Select One
Two circles with centres A and B of radii 3 cm and 4 cm respectively intersect at two points C and D, such that AC and BC are tangents to the two circle. Find the length of the common chord CD.
A4.2 cmB8.4 cmC2.4 cmD4.8 cm - Question 3 - Select One
Two circles intersect at A and B. P is a point on produced BA. PT and PQ are tangents to the circles. The relation of PT and PQ is
APT = 2PQBPT<PQCPT>PQDPT=PQ
Two line segments may intersect at two points
View SolutionTwo circle intersect in AandBandACandAD are respectively the diameters of the circles. Prove that C,B,D are collinear.
View SolutionTwo circles intersect each other at point P an Q. If PA and PB are two diameter then find ∠AQB.
View SolutionTwo circles intersect at two points P and S. QR is a tangent to the two circles at Q and R. If ∠QSR=72∘, then ∠QPR=.
View SolutionTwo circles are drawn with sides AB,AC of a triangle ABC as diameters. The circles intersect at a point D. Prove that D lies on BC.
View Solution

