Two different points P and Q are given on one side of line AB. Draw a circle passing through the points P and Q touching the line AB in point R.
To construct a circle passing through points P and Q that touches line AB at point R, follow these steps:
1. Draw Line AB: Start by drawing a horizontal line segment AB on your paper. This will be the line that the circle will touch.
2. Locate Points P and Q: Mark two different points P and Q on one side of line AB. Ensure that both points are above the line.
3. Draw a Circle: Using a compass, draw a circle that passes through points P and Q. The radius can be adjusted based on the distance between P and Q.
4. Find the Midpoint of Segment PQ: Use a ruler to measure the distance between points P and Q. Find the midpoint M of segment PQ.
5. Draw a Perpendicular Line: At point M, draw a perpendicular line to segment PQ. This line will help in finding the point R where the circle touches line AB.
6. Locate Point R on Line AB: Extend the perpendicular line downwards until it intersects line AB. Mark this intersection point as R.
7. Draw the Circle: Now, using point R as the center and the distance from R to either point P or Q as the radius, draw the circle. This circle will pass through points P and Q and touch line AB at point R.
Topper's Solved these Questions
- GEOMETRIC CONSTRUCTIONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - GEOMETRIC CONSTRUCTIONS EXERCISE - EXAMPLE
3 Videos
- GEOMETRIC CONSTRUCTIONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - GEOMETRIC CONSTRUCTIONS EXERCISE - LETS REVISE CERTAIN CONSTRUCTIONS STUDIED IN THE PREVIOUS STANDARDS
8 Videos
- GEOMETRIC CONSTRUCTIONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - GEOMETRIC CONSTRUCTIONS EXERCISE - Assigment 5.5
5 Videos
- FINANCIAL PLANNING BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - FINANCIAL PLANNING EXERCISE - ASSIGNEMENT 4.4
4 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - 4 Marks Questions
18 Videos
Similar Questions
Knowledge Check
P(a,5a) and Q(4a,a) are two points. Two circles are drawn through these points touching the axis of y.
Centre of these circles are atA(a,a),(2a,3a)B(205a18,29a3),(5a2,3a)C(3a,29a3),(205a9,29a18)DNone of theseP and Q are two points on circle with centre O. The point R is on the minor arcPQ. The tangents from P and Q meet at S. If ∠PSQ=20∘ them ∠PRQ is-
A80∘B200∘C160∘D100∘
Draw a line AB. Take a point P outside it. Draw a line passing through P and parallel to AB.
View SolutionDraw a line AB. Take a point P outside it. Draw a line passing through P and perpendicular to AB.
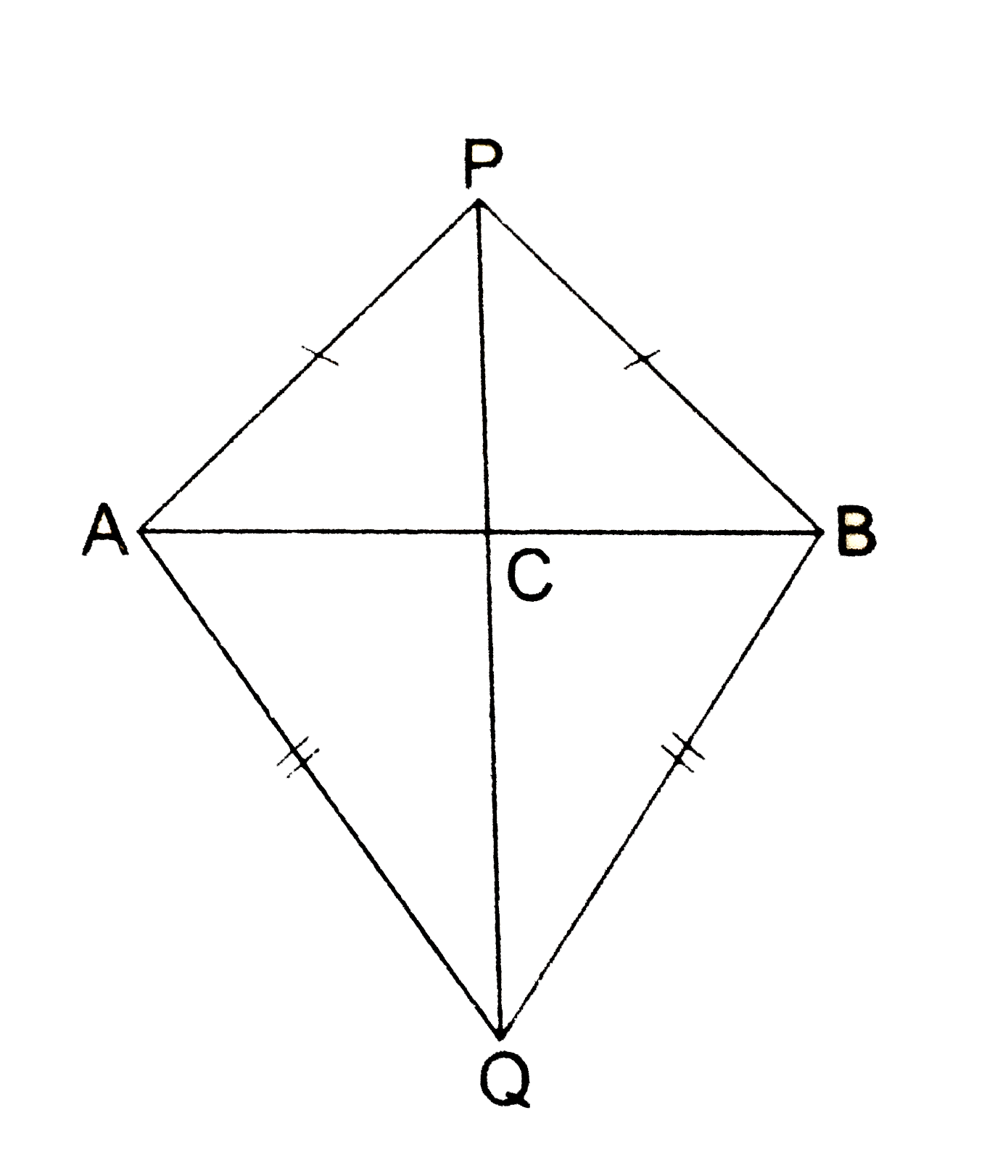
View SolutionIn the given figure, AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B. Show that the line PQ is the perpendicular bisector of AB.
View SolutionDraw a line AB. Take a point P on it. Draw a line passing through P and perpendicular to AB.
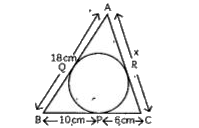
View SolutionIn the figure, all three sides of a triangle ABC touch the circle at points P, Q and R. Find the value of x.
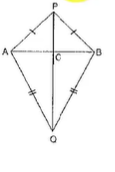
View SolutionAB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (in figure). Show that the line PQ is perpendicular bisector of AB
View Solution
