In the given figure, AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B. Show that the line PQ is the perpendicular bisector of AB.

Video Solution

Text Solution

Verified by Experts

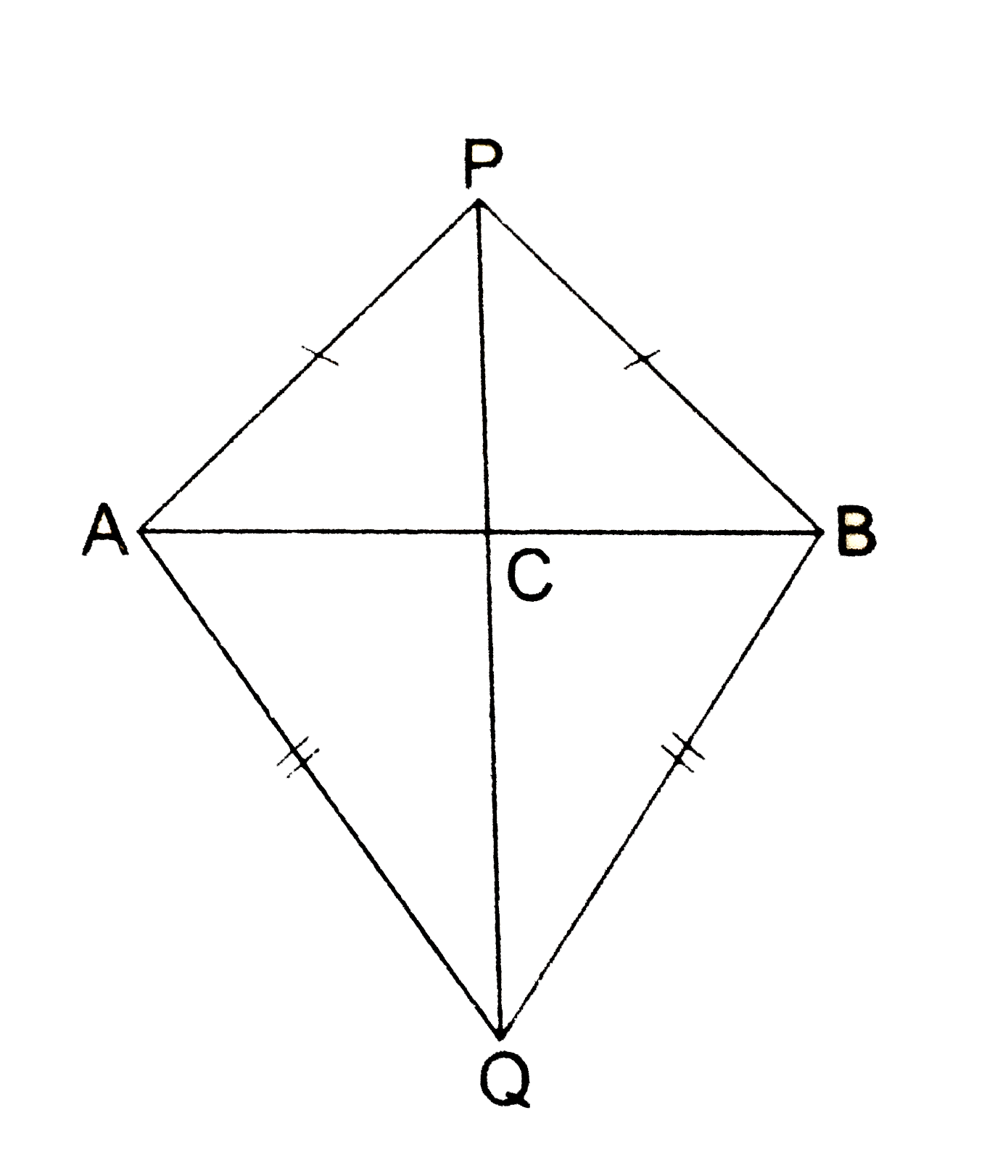
GIVEN A line segment AB and two point P and Q such that PA = PB and QA = QB.
TO PROVE Let AB and PQ intersect at C. Then, we have to prove that AC = BC and $∠ A C P = 90^{\circ}$ .
PROOF In $Δ P A Q and Δ P B Q,$ we have
$P A = P B (given)$
$O A = Q B (given)$
$P Q = P Q (common)$
$∴ Δ P A Q ≅ Δ P B Q (by SSS-criteria).$
$∴ ∠ A P Q = ∠ B P Q ...(i) (c.p.c.t.).$
Now, in $Δ P A C and Δ P B C,$ we have
$P A = P B (given)$
$∠ A P C = ∠ B P C [∵ ∠ A P Q = ∠ B P Q in (i)]$
$P C = P C (common)$
$∴ Δ P A C ≅ Δ P B C (by SAS-criteria).$
$∴ A C = B C ...(ii) (c.p.c.t.).$
And, $∠ A C P = ∠ B C P ...(iii) (c.p.c.t.).$
But, $∠ A C P + ∠ B C P = 180^{\circ} (linear pair).$
$∴ 2 ∠ A C P = 180^{\circ} [using (iii)].$
So, $∠ A C P = 90^{\circ} .$
Hence, PQ is the perpendicular bisector of AB.

Updated on:21/07/2023

|

Class 9 MATHS CONGRUENCE OF TRIANGLES

Topper's Solved these Questions

Similar Questions

RS AGGARWAL-CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE-Multiple Choice Questions (Mcq)

Home
Ask Doubt
Profile