Two lines AB and CD intersect each other at a point O such that ∠AOC:∠AOD=5:7. Find all the angles.
The correct Answer is:∠AOC=75∘=∠BOD,∠AOD=105∘=∠BOC
To solve the problem, we need to find the angles formed by the intersection of two lines AB and CD at point O, given that the ratio of angles AOC to AOD is 5:7.
1. Define the Angles:
Let angle AOC = 5x and angle AOD = 7x, where x is a common multiplier.
Hint: Use variables to represent the angles based on the given ratio.
2. Use the Straight Line Property:
Since angles AOC and AOD are on a straight line (CD), we know that:
angle AOC+angle AOD=180∘
Substituting the values we defined:
5x+7x=180∘
Hint: Remember that angles on a straight line sum up to 180 degrees.
3. Combine Like Terms:
Combine the terms on the left side:
12x=180∘
Hint: Simplify the equation to isolate x.
4. Solve for x:
Divide both sides by 12:
x=180∘12=15∘
Hint: Perform the division carefully to find the value of x.
5. Calculate the Angles:
Now, substitute x back into the expressions for the angles:
- Angle AOC:
angle AOC=5x=5×15∘=75∘
- Angle AOD:
angle AOD=7x=7×15∘=105∘
Hint: Use the value of x to find each angle separately.
6. Find the Vertically Opposite Angles:
Since angles AOC and AOD are vertically opposite to angles BOD and COB respectively:
- Angle BOD = Angle AOC = 75°
- Angle COB = Angle AOD = 105°
Hint: Recall that vertically opposite angles are equal.
Final Angles:
- Angle AOC = 75°
- Angle AOD = 105°
- Angle BOD = 75°
- Angle COB = 105°
Summary:
All angles formed by the intersection of lines AB and CD at point O are:
- Angle AOC = 75°
- Angle AOD = 105°
- Angle BOD = 75°
- Angle COB = 105°
Let angle AOC = 5x and angle AOD = 7x, where x is a common multiplier.
Since angles AOC and AOD are on a straight line (CD), we know that:
angle AOC+angle AOD=180∘
Substituting the values we defined:
5x+7x=180∘
Combine the terms on the left side:
12x=180∘
Divide both sides by 12:
x=180∘12=15∘
Now, substitute x back into the expressions for the angles:
- Angle AOC:
angle AOC=5x=5×15∘=75∘
- Angle AOD:
angle AOD=7x=7×15∘=105∘
Since angles AOC and AOD are vertically opposite to angles BOD and COB respectively:
- Angle BOD = Angle AOC = 75°
- Angle COB = Angle AOD = 105°
- Angle AOC = 75°
- Angle AOD = 105°
- Angle BOD = 75°
- Angle COB = 105°
All angles formed by the intersection of lines AB and CD at point O are:
- Angle AOC = 75°
- Angle AOD = 105°
- Angle BOD = 75°
- Angle COB = 105°
Topper's Solved these Questions
- LINES AND ANGLESBOOK - RS AGGARWALCHAPTER - LINES AND ANGLESEXERCISE - Exercise 7C
24 Videos
- LINES AND ANGLESBOOK - RS AGGARWALCHAPTER - LINES AND ANGLESEXERCISE - Multiple Choice Questions (Mcq)
28 Videos
- LINES AND ANGLESBOOK - RS AGGARWALCHAPTER - LINES AND ANGLESEXERCISE - Exercise 7A
12 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBOOK - RS AGGARWALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Multiple Choice Questions (Mcq)
24 Videos
- MEAN , MEDIAN AND MODE OF UNGROUPED DATA BOOK - RS AGGARWALCHAPTER - MEAN , MEDIAN AND MODE OF UNGROUPED DATA EXERCISE - Multiple Choice Questions (Mcq)
18 Videos
Similar Questions
Knowledge Check
The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC=32∘and∠AOB=70∘, find ∠DBC.
A35∘B38∘C40∘D45∘
In the given figure, three lines AB, CD and EF intersect at a point O such that ∠AOE=35∘ and ∠BOD=40∘. Find the measure of ∠AOC,∠BOF,∠COF and ∠DOE.
View SolutionTwo lines AB and CD intersect at point O. ∠AOD:∠BOD=3:1, then ∠AOD=…………………
View SolutionIf two lines AB and CD intersect at O such that ∠AOC=5∠AOD, then the four angles at O are
View SolutionTwo lines "AB" and "CD" intersect at a point O such that ∠BOC+∠AOD=280∘, as shown in the figure. Find all four angles.
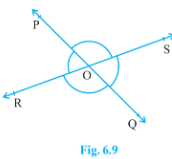
View SolutionLines PQ and RS intersect each other at point O. If ∠POR:∠ROQ=5:7, find all the angles.
View SolutionIn Fig: 6.9. lines PQ and RS intersect each other at point O. If ∠POR:∠ROQ=5:7,find the all the angles..
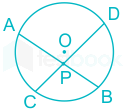
View SolutionIn the given figure, O is the centre of the circle. Its two chords AB and CD intersect each other at the point p within the circle. If AB=15cm,PB=9cm, then find the length of PD.
View Solution
