Two number aandb are chosen at random from the set of first 30 natural numbers. Find the probability that a2−b2 is divisible by 3.Solution in Bengali
The correct Answer is:4787
The total number of ways of choosing two numbers out of 1, 2, 3, …, 30 is .30C2 = 435.
Now, 30 natural numbers are categorized as
3k type: 3, 6, 9, … 30 → 10 numbers
3k + 1 type: 1, 4, 7, …, 28 → 10 numbers
3k + 2 type: 2, 5, 8, ..., 29 → 10 numbers
a2−b2 is divisible by 3 iff either both of a and b are So, number of favourable cases = .10C2+.20C2=235
∴ Required probability = 235435=4787
Topper's Solved these Questions
- PROBABILITY I BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Exercise 9.3
7 Videos
- PROBABILITY I BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - MCQ
54 Videos
- PROBABILITY I BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Exercise 9.1
6 Videos
- PROBABILITYBOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITYEXERCISE - All Questions
470 Videos
- PROBABILITY IIBOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY IIEXERCISE - MULTIPLE CORRECT ANSWER TYPE
6 Videos
Similar Questions
AandB are two candidates seeking admission in IIT. The probability that A is selected is 0.5 and the probability that AandB are selected is at most 0.3. Is it possible that the probability of B getting selected is 0.9?
View SolutionA sample space consists of 3 sample points with associated probabilities given as 2p,p2,4p−1. Then the value of p is p= a.√11−3 b. √10−3 c. 14<p<12 d.none
View SolutionWhich of the following cannot be valid assignment of probabilities for outcomes of sample space S={W1,W2,W3,W4,W5,W6,W7}
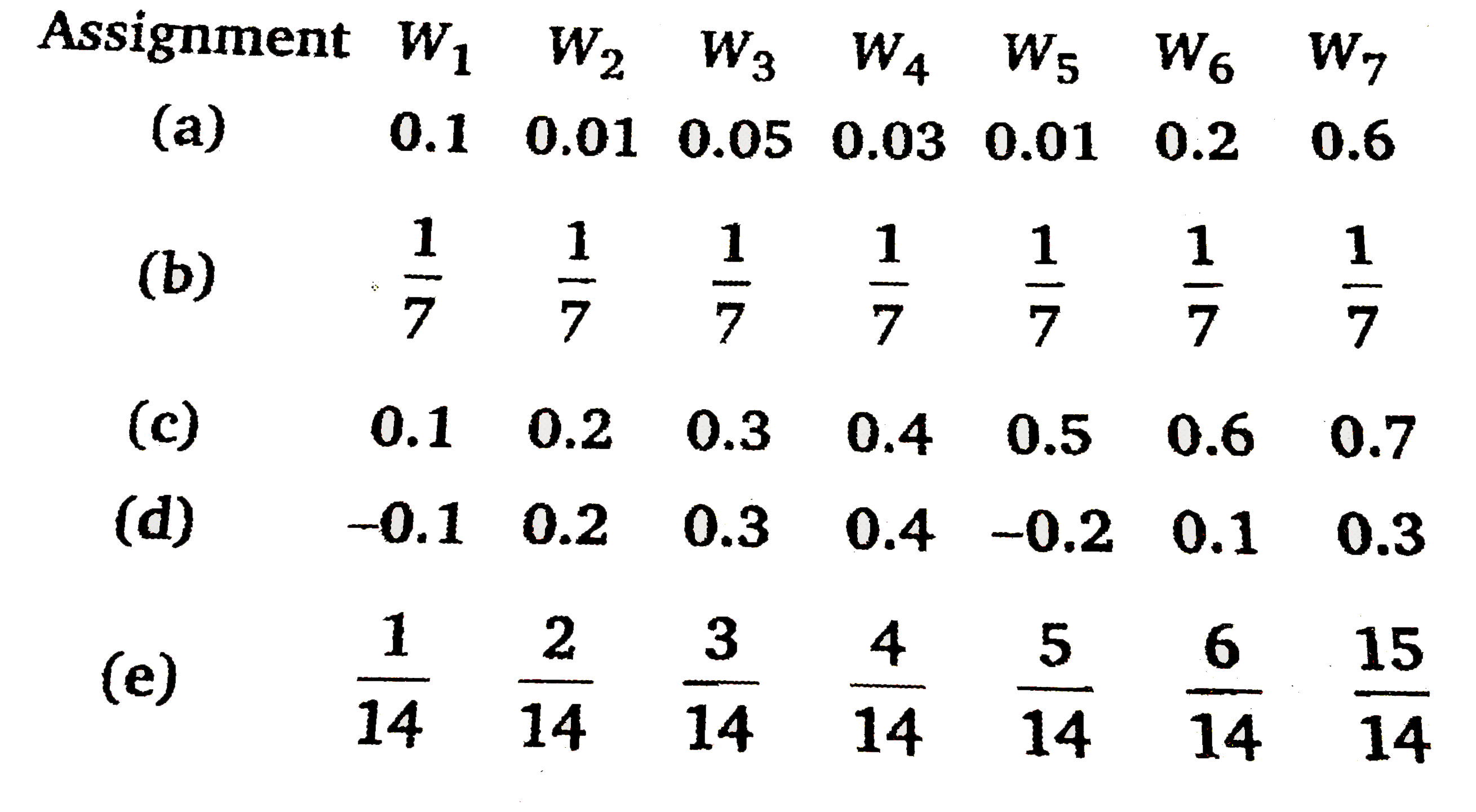
View SolutionA coin is tossed three times, consider the following events. A : ‘No head appears’, B: ‘Exactly one head appears’ and C: ‘Atleast two appear’. Do they form a set of mutually exclusive and exhaustive events?
View SolutionLet EandF be two independent events. The probability that exactly one of them occurs is 1125 and the probability if none of them occurring is 225. If P(T) denotes the probability of occurrence of the event T, then (a) P(E)=45,P(F)=35 (b) P(E)=15,P(F)=25 (c) P(E)=25,P(F)=15 (d) P(E)=35,P(F)=45
View SolutionTwo number aandb aer chosen at random from the set of first 30 natural numbers. Find the probability that a2−b2 is divisible by 3.
View SolutionTwo natural numbers x and y are chosen at random from the set {1,2,3,4,...3n}. find the probability that x^(2)-y^(2) is divisible by 3.
View SolutionA natural number is chosen at random from amongst first 500. What is the probability that the number so chosen is divisible by 3 or 5?
View SolutionTwo numbers a and b are chosen at random from the set {1,2,3,..,3n}. The probability that a3+b3 is divisible by 3, is
View SolutionTwo numbers a and b are chosen at random from the set of first 30 natural numbers. The probability that a2−b2 is divisible by 3 is
View SolutionA natural number is chosen at random from amongst the first 300. what is the probability that the number , so chosen is divisible by 3 or 5 ?
View SolutionA sum of money doubles in 3 years at compound interest compounded annually. It will becomes 4 times of itself in:
View SolutionTwo number aandb aer chosen at random from the set of first 30 natural numbers. Find the probability that a2−b2 is divisible by 3.
View SolutionA natural number is chosen at random from amongst first 500. What is the probability that the number so chosen is divisible by 3 or 5?
View SolutionA natural number is chosen at random from amongst the first 300. what is the probability that the number , so chosen is divisible by 3 or 5 ?
View SolutionA natural number is chosen at random from the first 100 natural numbers. What is the probability that the number chosen is a multiple of 2 or 3 or 5?
View Solution
