Two numbers whose sum is 12 and the absolute value of whose difference is 4 are the roots of the equation____
x2−12x+30=0
x2−12x+32=0
2x2−6x+7=0
2x2−24x+43=0
The correct Answer is:B
To find the quadratic equation whose roots are two numbers whose sum is 12 and the absolute value of whose difference is 4, we can follow these steps:
Step 1: Define the Variables
Let the two numbers be α and β.
Step 2: Set Up the Equations
From the problem, we know:
1. The sum of the numbers:
α+β=12
2. The absolute value of the difference of the numbers:
|α−β|=4
This gives us two cases:
- Case 1: α−β=4
- Case 2: β−α=4
Step 3: Solve the Equations
Case 1: α−β=4
We can add the two equations:
α+β=12(1)
α−β=4(2)
Adding (1) and (2):
(α+β)+(α−β)=12+4
2α=16
α=8
Now substitute α=8 back into equation (1):
8+β=12
β=12−8=4
So, in this case, the two numbers are α=8 and β=4.
Case 2: β−α=4
We can also solve this case similarly:
α+β=12(1)
β−α=4(3)
Adding (1) and (3):
(α+β)+(β−α)=12+4
2β=16
β=8
Now substitute β=8 back into equation (1):
α+8=12
α=12−8=4
So, in this case, the two numbers are α=4 and β=8.
Step 4: Form the Quadratic Equation
The roots of the quadratic equation can be expressed using the formula:
x2−(α+β)x+αβ=0
Substituting α+β=12 and αβ=8×4=32:
x2−12x+32=0
Final Answer
The quadratic equation whose roots are the two numbers is:
x2−12x+32=0
Let the two numbers be α and β.
From the problem, we know:
1. The sum of the numbers:
α+β=12
2. The absolute value of the difference of the numbers:
|α−β|=4
This gives us two cases:
- Case 1: α−β=4
- Case 2: β−α=4
Case 1: α−β=4
We can add the two equations:
α+β=12(1)
α−β=4(2)
(α+β)+(α−β)=12+4
2α=16
α=8
8+β=12
β=12−8=4
We can also solve this case similarly:
α+β=12(1)
β−α=4(3)
(α+β)+(β−α)=12+4
2β=16
β=8
α+8=12
α=12−8=4
The roots of the quadratic equation can be expressed using the formula:
x2−(α+β)x+αβ=0
x2−12x+32=0
The quadratic equation whose roots are the two numbers is:
x2−12x+32=0
Topper's Solved these Questions
- QUADRATIC EQUATIONSBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - QUADRATIC EQUATIONSEXERCISE - Everyday Mathematics
4 Videos
- QUADRATIC EQUATIONSBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - QUADRATIC EQUATIONSEXERCISE - Achievers Section (HOTS)
3 Videos
- PROBABILITYBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - PROBABILITYEXERCISE - ACHIEVERS SECTION (HOTS)
3 Videos
- REAL NUMBERSBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - REAL NUMBERSEXERCISE - EVERYDAY MATHEMATICS
7 Videos
Similar Questions
Consider the graph of y = f(x) as shown in the following figure.
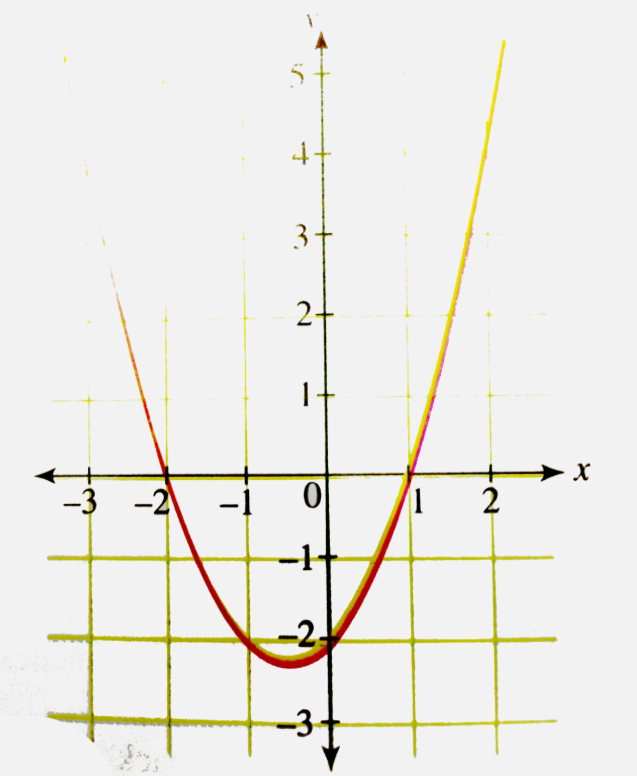
(i) Find the sum of the roots of the equation f (x) = 0.
(ii) Find the product of the roots of the equation f(x) = 4.
(iii) Find the absolute value of the difference of the roots of the equation f(x) = x+2 .
View SolutionFind two numbers whose sum is 27 and product is 182.
View Solution
Knowledge Check
Two numbers whose sum is 8 and difference is4, are the roots of the equation
Ax2+8x+12=0Bx2+8x−12=0Cx2−8x−12=0Dx2−8x+12=0Two numbers whose sum is 84 can not be in the ratio
A5:7B13:8C1:3D3:2Two numbers whose sum is 84 can not be in the ratio
A5:7B13:8C1:3D3:2
Find two positive numbers whose sum is 16 and the sum of whose cubes is minimum.
View Solutionfind the two numbers whose sum is 100 and whose ratio is 9:16
View SolutionFind two numbers whose sum is 100 and whose ratio is 9 :16.
View SolutionTwo numbers whose sum is 84 can not be in the ratio
View SolutionTwo whole numbers, whose sum is 64, can not be in the ratio:
View Solution
