Two parallel lines AB and CD are intersected by a transversal line EF at M and N, respectively. If the lines MP and NP are the bisectors of the interior angles BMN and DNM on the same side of the transversal, then ∠MPN is equal to
180∘
60∘
90∘
None of these
The correct Answer is:C
To solve the problem, we need to find the measure of angle MPN given that MP and NP are the angle bisectors of angles BMN and DNM respectively, formed by the intersection of the transversal EF with the parallel lines AB and CD.
1. Identify the Angles:
- Let ∠BMN=x and ∠DNM=y.
- Since AB and CD are parallel lines and EF is a transversal, the interior angles on the same side of the transversal are supplementary:
x+y=180∘(1)
2. Find the Bisected Angles:
- The angle bisector MP divides ∠BMN into two equal parts:
∠PMN=x2(2)
- The angle bisector NP divides ∠DNM into two equal parts:
∠PNM=y2(3)
3. Substitute into the Supplementary Angles:
- From equation (1), we can express y:
y=180∘−x
- Substitute y into equation (3):
∠PNM=180∘−x2=90∘−x2(4)
4. Sum of Angles in Triangle PMN:
- In triangle PMN, the sum of the angles is:
∠PMN+∠PNM+∠MPN=180∘(5)
- Substitute equations (2) and (4) into equation (5):
x2+(90∘−x2)+∠MPN=180∘
- Simplifying this:
90∘+∠MPN=180∘
- Therefore:
∠MPN=180∘−90∘=90∘
Conclusion:
Thus, the measure of angle MPN is 90∘.
- Let ∠BMN=x and ∠DNM=y.
- Since AB and CD are parallel lines and EF is a transversal, the interior angles on the same side of the transversal are supplementary:
x+y=180∘(1)
- The angle bisector MP divides ∠BMN into two equal parts:
∠PMN=x2(2)
- The angle bisector NP divides ∠DNM into two equal parts:
∠PNM=y2(3)
- From equation (1), we can express y:
y=180∘−x
- Substitute y into equation (3):
∠PNM=180∘−x2=90∘−x2(4)
- In triangle PMN, the sum of the angles is:
∠PMN+∠PNM+∠MPN=180∘(5)
- Substitute equations (2) and (4) into equation (5):
x2+(90∘−x2)+∠MPN=180∘
- Simplifying this:
90∘+∠MPN=180∘
- Therefore:
∠MPN=180∘−90∘=90∘
Thus, the measure of angle MPN is 90∘.
Topper's Solved these Questions
- GEOMETRYBOOK - ARIHANT PUBLICATION JHARKHANDCHAPTER - GEOMETRYEXERCISE - Exam Booster For Cracking Exam
20 Videos
- FACTORISATION OF POLYNOMIALSBOOK - ARIHANT PUBLICATION JHARKHANDCHAPTER - FACTORISATION OF POLYNOMIALSEXERCISE - Exam Booster for Cracking Exam
30 Videos
- HCF AND LCMBOOK - ARIHANT PUBLICATION JHARKHANDCHAPTER - HCF AND LCMEXERCISE - Exam Booster for Cracking Exam
24 Videos
Similar Questions
Two parallel lines l and m are intersected by a transversal p (see Fig. 8.15). Show that the quadrilateral formed by the bisectors of interior angles is a rectangle.
View SolutionFill in the blanks in each of the following to make the statement true: (i) If two parallel lines are intersected by a transversal, then each pair of corresponding angles are.... (ii) If two parallel lines are intersected by a transversal, then interior angles on the same side of the transversal are... (iii) Two lines perpendicular to the same line are.... to each other. (iv) Two lines parallel to the same line are .......... to each other. (v) If a transversal intersects a pair of lines in such away that a pair of alternate angles are equal, then the line are... (vi) If a transversal intersects a pair of lines in such away that the sum of interior angles on the same side of transversal is 180,then the line are .......
View Solution
Knowledge Check
Two parallel lines AB and CD are intersected by a transversal line EF at M and N, respectively. If the lines MP and NP are the bisectors of the interior angles BMN and DNM on the same side of the transversal, then ∠MPN is equal to
A180∘B60∘C90∘Dnone of theseTwo parallel lines AB and CD are intersected by a transversal EF at M and N respectively.
The lines MP and NP are the bisectors of interior angles ∠BMN and ∠DNM on the same side of the transversal. Then ∠MPN is equal to :A60∘B90∘C45∘D120∘Two parallel lines AB and CD are intersected by a transversal EF at M and N respectively.
The lines MP and NP are the bisectors of interior angles ∠BMN and ∠DNM on the same side of the transversal. Then ∠MPN is equal to :A60∘B90∘C45∘D120∘
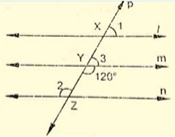
In Fig. l, m and n are parallel lines intersected by transversal p at X, Y and Z respectively. Find ∠1, ∠2 and ∠3
View SolutionIf two parallel lines are intersected by a transversal , then the interior angles on the same side of the transversal are -
View SolutionIf two lines are intersected by a transversal, then the number of pairs of interior angles on the same side of the transversal is
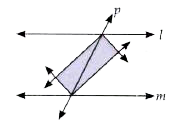
View SolutionTwo parallel line l and m are intersected by a transversal p. The quadrilateral formed by the bisectors of interior angles is a
View SolutionAB and CD are two parallel lines and a transversal PO intersects AB and CD at M and N respectively. The bisector of the interior angles form a quadrilateral :

View Solution
