Two parallel lines lying in the same quadrant make intercepts a and b on x and y axes, respectively, between them. The distance between the lines is (a) ab√a2+b2 (b) √a2+b2 (c) 1√a2+b2 (d) 1a2+1b2
A
√a2+b2
B
ab√a2+b2
C
1√a2+b2
D
1a2+1b2
Video Solution
Text Solution
The correct Answer is:B
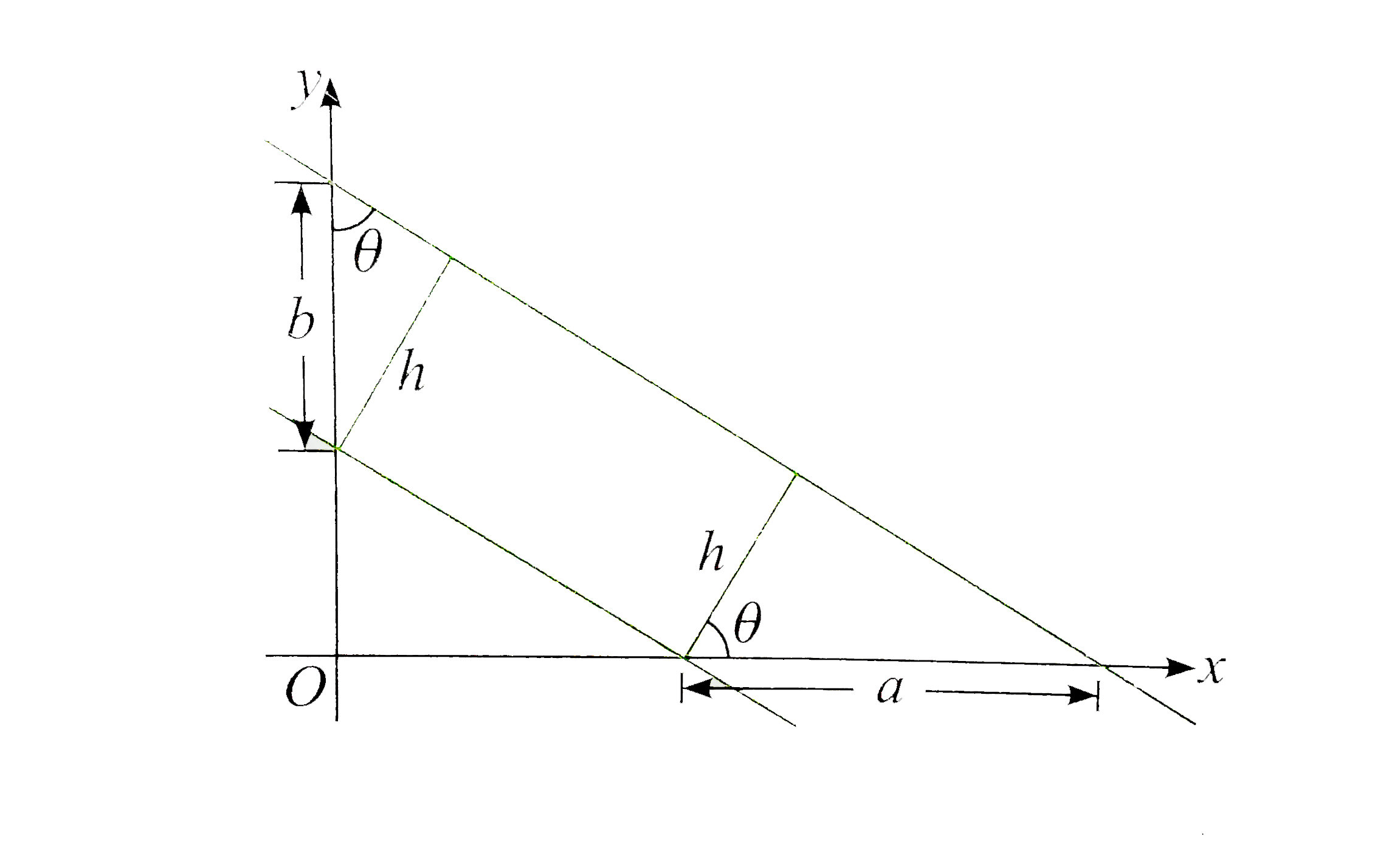
From the figure
cosθ=ha and sinθ=hb
Squaring these and then adding, we get
1=h2a2+h2b2
∴h=ab√a2+b2
|
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Multiple)
30 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Comprehension)
27 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.6
5 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
Knowledge Check
The shortest distance between the line x=y and the curve y2=x−2 is
A2B78C74√2D114√2If x=√a+2b+√a−2b√a+2b−√a−2b then bx2+b =
AaxB0C−axD−1The angle between two vectors a and b with magnitudes √3and2 respectively, having a.b=√6 is
Aπ4Bπ2Cπ6Dπ3
The minimum vertical distance between the graphs of y=2+sinx and y=cosx is (a)2 (b)1 (c) √2 (d) 2−√2
View SolutionThe distance of the point P(a, b, c) from the x-axis is a. √b2+c2 b. √a2+c2 c. √a2+b2 d. none of these
View SolutionShow that the distance between the parallel lines ax+by+c=0 and k(ax+by)+d=0 is ∣∣ ∣∣c−dk√a2+b2∣∣ ∣∣
View SolutionDistance of the points (a,b,c) for the y axis is
(a) √b2+c2(b)√c2+a2(c)√a2+b2(d)√a2+b2+c2
View SolutionThe area included between the parabolas y2=4ax(x+a)andy2=4b(b−x)is83√ab(a+b).True False
View Solution
