Two pillars of equal height and on either side of a road, which is 100 m wide. The angles of elevation of the top of the pillars are 60∘ and 30∘ at a point on the road between the pillars. Find the height of each pillar.
34.5 m
25.4 m
43.3 m
75 m
The correct Answer is:C
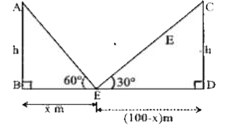
Let AB and CD be two pillars, each of height h metres and AC be the road that AC=100m.
Let O be the point of observation on AC.
Also, ∠AOB=60∘ and ∠COD=30∘,
AB⊥AC and CD⊥AC.
From right ΔOAB, we have
ABOA=tan60∘=√3
⇒hx=√3⇒h=√3x..........(i).
From right ΔOCD, we have
CDOC=tan30∘=1√3.
rARrh(100−x)=1√3⇒h=(100−x)√3.......(ii)
Equating the values of h from (i) and (ii) , we get
√3x=(100−x)√3⇒3x=(100−x)⇒4x=100⇒x=25.
Putting x=25m in (i), we get
h=(25×√3)=(25×1.732)=43.3.
Hence, the height of each pillar is 43.3m and the point of observation is 25m away from the first pillar.

Topper's Solved these Questions
- HEIGHTS AND DISTANCESBOOK - RS AGGARWALCHAPTER - HEIGHTS AND DISTANCESEXERCISE - Exercise 14
38 Videos
- HEIGHTS AND DISTANCESBOOK - RS AGGARWALCHAPTER - HEIGHTS AND DISTANCESEXERCISE - Multiple Choice Questions (Mcq)
25 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
34 Videos
- LINEAR EQUATIONS IN TWO VARIABLES BOOK - RS AGGARWALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - QUESTION
2 Videos
Similar Questions
Two pillars of equal height and on either side of a road, which is 100m wide. The angles of elevation of the top of the pillars are 60o and 30o at a point on the road between the pillars. Find the position of the point between the pillars and the height of each pillar.
View SolutionTwo pillars of equal height and on either side of a road, which is 100m wide. The angles of elevation of the top of the pillars are 60o and 30o at a point on the road between the pillars. Find the position of the point between the pillars and the height of each pillar.
View Solution
Knowledge Check
Two pillars of equal height stand on either side of a road way which is 60 m wide. At a point in the road way between the pillars, the elevation of the top of pillars are 60∘ and 30∘. The height of the pillars is :
A15√3 mB15√3 mC15 mD20 mTwo pillars of equal height stand on either side of a road way which is 60 m wide. At a point in the road way between the pillars, the elevation of the top of pillars are 60∘ and 30∘. The height of the pillars is :
A15√3 mB15√3 mC15 mD20 mTwo pillars of equal height stand on either side of a road-way which is 60m wide. At a point in the road-way between the pillars, the elevation of its top of pillars are 60∘ and 30∘. The height of the pillars is
A15√3mB15√3mC15 mD20 m
Two pillars of equal height are on either side of a road, which is 100 m wide. The angles of elevation of the top of the pillar are 60∘and30∘ at a point on the road between the pillars. Find the position of the point between the pillars and the height of each pillar.
View SolutionTwo pillars of equal heights stand on either side of a road which is 100 m wide. At a point on the road between the pillars, the angles of elevations of the tops of the pillars are 30∘and45∘. Find the height of each pillar and position of the point on the road.
View SolutionTwo pillars of equal height are on either side of a roadway which is 30 m wide. At a point on the roadway between the pillars, the elevations of the top of the pillars are 60∘ and 30∘. Find the height of the pillars and the position of the point.
View SolutionTwo pillars of equal height stand on either side of a roadway which is 120 m wide. At a point in the road between the pillars, the angles of elevation of the pillars are 60∘ and 30∘. Find the height of each pillars to the nearest metre and position of the point from both the pillars.
View SolutionTwo poles of equal heights are standing opposite to each other on either side of the road , which is 100 m wide . From a point between them on the road , the angles of elevation of the top of the poles are 60∘and30∘ respectively .Find the height of the poles .
View Solution
