Two poles of equal heights are standing opposite each other on either side of the road, which is 80m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘and30∘, respectively. Find the height of the poles and the distances of the point from the poles.
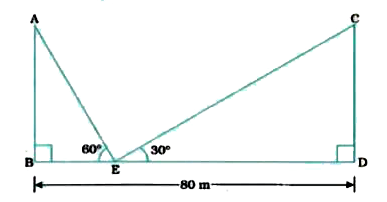 Solution in Gujrati
Solution in Gujrati
The correct Answer is:20√3m
Step by step video, text & image solution for Two poles of equal heights are standing opposite each other on either side of the road, which is 80m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60^(@) and 30^(@), respectively. Find the height of the poles and the distances of the point from the poles. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SOME AAPLICATIONS OF TRIGONOMETRYBOOK - KUMAR PRAKASHANCHAPTER - SOME AAPLICATIONS OF TRIGONOMETRYEXERCISE - Test Your Skills
5 Videos
- SOME AAPLICATIONS OF TRIGONOMETRYBOOK - KUMAR PRAKASHANCHAPTER - SOME AAPLICATIONS OF TRIGONOMETRYEXERCISE - Practice Thoroughly
7 Videos
- SOME AAPLICATIONS OF TRIGONOMETRYBOOK - KUMAR PRAKASHANCHAPTER - SOME AAPLICATIONS OF TRIGONOMETRYEXERCISE - Other Important Examples
3 Videos
- REAL NUMBERS BOOK - KUMAR PRAKASHANCHAPTER - REAL NUMBERS EXERCISE - TEST YOUR SKILLS
26 Videos
- STATISTICSBOOK - KUMAR PRAKASHANCHAPTER - STATISTICSEXERCISE - Objective Questions (True or false)
5 Videos
Similar Questions
The angle of elevation of the top of a tower 30m high from the foot of another tower in the same plane is 60∘ and the angle of elevation of the top the second tower from the foot of the first tower is 30∘. Find the distance between the two towers and also find the height of the other tower.
View SolutionA jet plane is at a vertical height of h. The angles of depression of two tanks on the ground in the same line with the plane are αandβ(α>β). Prove that the distance between the tanks is h(tanα−tanβ)tanαtanβ
View SolutionA building stands on a horizontal plane and is surmounted by a vertical flag-stagg of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flag-staff are αandβ respectively. Prove that the height of the building is htanαtanβ−tanα
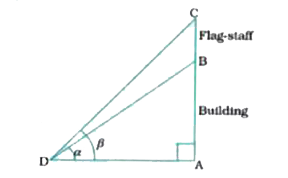
View SolutionShow that the square of any positive integer is of the form 4m or 4m + 1 for some integer m.
View SolutionFor any frequency distribution, mean is always greater than mode.
View SolutionTwo poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘and 30∘, respectively. Find the height of the poles and the distances of the point from the poles.
View SolutionTwo poles of equal heights are standing opposite to each other on either side of the road which is 80 m wide. From a point between them on the road the angles of elevation of the top of the poles are 60∘ and 30∘ respectively. Find the height of the poles and the distances of the point from the poles.
View SolutionTwo poles of equal heights are standing opposite to each other on either side of the road which is 80 m wide. From a point P between them on the road, the angle of elevation of the top of one pole is 60∘ and the angle of depression from the top of another pole is 30∘ find the height of pole and distances of the point P from the poles.
View SolutionTwo poles of equal height are standing opposite to each other on either sidef of the road, which is 120 feet wide. From a point between then on the road, the angles of elevation of the top of the poles are 60∘ and 30∘ respectively. Find the height of the poles and the distances of the point from the poles.
View SolutionTwo poles of equal height are standing opposite to each other on either side of the road, which is 80 m wide. From a point between then on the road, the angles of elevation of top of the poles are 60∘ and 30∘. Find the height of poles.
View SolutionTwo poles of equal heights are standing opposite each other on either side of the road, which is 80m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘ and 30∘, respectively . Find the height of the poles and the distances of the point from the poles.
View SolutionTwo poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘ to 30∘, respectively. Find the height of the poles and the distances of the point from the poles.
View SolutionTwo poles of equal heights are standing opposite to each other on either side of the road, which is 120 feet wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘ and 30∘ respectively. Find the height of the poles and the distances of the point from the poles.
View SolutionTwo poles of equal heights are standing opposite to each other on either side of the road, which is 120 feet wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘ and 30∘ respectively. Find the height of the poles and the distances of the point from the poles.
View SolutionTwo poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘and 30∘, respectively. Find the height of the poles and the distances of the point from the poles.
View Solution
