Two sides of a rhombus lying in the first quadrant are given by 3x−4y=0and12x−5y=0 . If the length of the longer diagonal is 12, then find the equations of the other two sides of the rhombus.Solution in Tamil
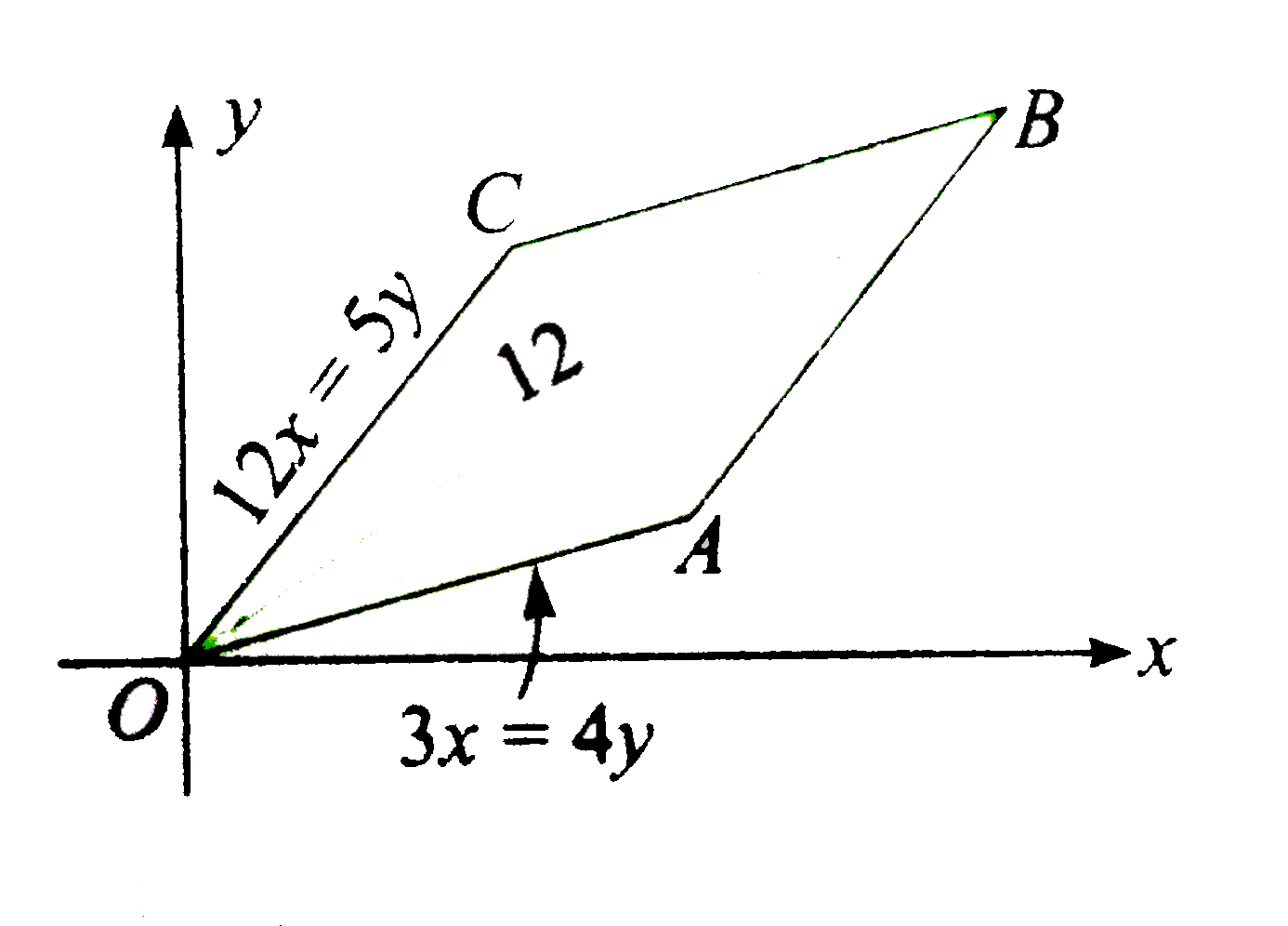
OB is along the acute angle bisector of the given lines: 3x-4y=0 and 12x-5y =0.
The equation of acute angle bisector is
3x−4y5=−12−5y13
or 9x-7y=0
∴Slope of OB=tanθ=97
Now, OB= 12.
Therefore, the coordinates of B are
(12cosθ,12sinθ)≡(127√130,129√130)≡(84√130,108√130)
AB is passing through B and is parallel to OC.
Therefore, the equation of AB is
y−108√130=125(x−84√130)
BC is passing through B and is parallel to OA.
Therefore, the equation of BC is y−108√130=34(x−84√130)
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.1
23 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.2
4 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
Find the equation of the right bisector of the line segment joining the points (3,4) and (−1,2).
View SolutionFind the points on the line x + y = 1 that lie at a distance 3 units from the line 5x+12y = 3.
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionQ. Let p and q real number such that p≠0,p2≠q and p2≠−q. if α and β are non-zero complex number satisfying α+β=−p and α3+β3=q, then a quadratic equation having αβ and βα as its roots is
View SolutionThe combined equation of two adjacent sides of a rhombus formed in first quadrant is 7x^(2)-8xy+y^(2)=0 then slope of its longer diagonal is
View SolutionIf the two sides of rhombus are x+2y+2=0 and 2x+y−3=0, then find the slope of the longer diagonal.
View SolutionTwo sides of a rhombus lying in the first quadrant are given by 3x−4y=0 and 12x−5y=0. If the length of the longer diagonal is 12, then find the equations of the other two sides of the rhombus.
View SolutionTwo sides of a rhombus lyin in the first quadrant are given by 3x−4y=0and12x−5y=0. If the length of the longer diagonal is 12 units, find the equationsof the other two sides of the rhombus.
View SolutionIf the two sides of rhombus are x+2y+2=0 and 2x+y−3=0, then find the slope of the longer diagonal.
View SolutionTwo sides of a rhombus lying in the first quadrant are given by 3x−4y=0 and 12x−5y=0. If the length of the longer diagonal is 12, then find the equations of the other two sides of the rhombus.
View SolutionTwo sides of a rhombus lying in the first quadrant are given by 3x−4y=0and12x−5y=0 . If the length of the longer diagonal is 12, then find the equations of the other two sides of the rhombus.
View SolutionIf the two sides of rhombus are x+2y+2=0 and 2x+y−3=0, then find the slope of the longer diagonal.
View SolutionTwo sides of a rhombus lying in the first quadrant are given by 3x-4y=0 and 12x-5y=0. The length of the longer diagonal is 12. If the equations of other two sides are 3x−4y+180√a=0and12x−5y=468√a then a−4010=
View SolutionThe combined equation of two adjacent sides of a rhombus formed in first quadrant is 7x2−8xy+y2=0 then slope of its longer diagonal is
View SolutionThe combined equation of two adjacent sides of a rhombus formed in first quadrant is 7x2−8xy+y2=0 then slope of its longer diagonal is
View Solution
