Two straight lines rotate about two fixed points (-a, 0) and (a, 0) in antic clockwise direction. If they start from their position of coincidence such that one rotates at a rate double of the other, then locus of curve is
Let PB make angle and PA make angle with x-axis.
Let P be (h,k).
(1)
(2)
From (2), we get
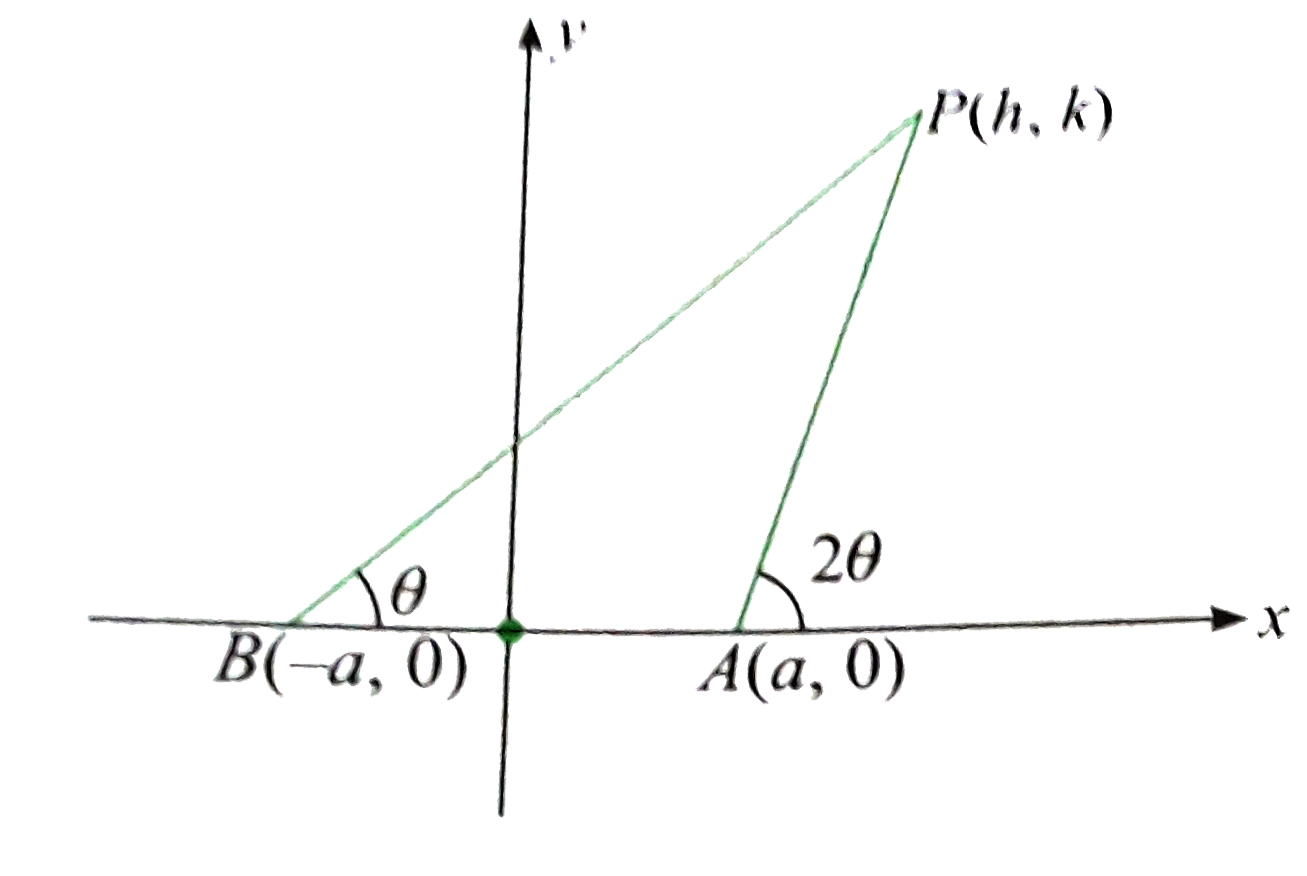
Putting value of from (1),we get
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.1
6 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.2
8 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
Two rods are rotating about two fixed points in opposite directions. If they start from their position of coincidence and one rotates at the rate double that of the other, then find the locus of point of the intersection of the two rods.
View SolutionTwo straight lines pass through the fixed points (±a,0) and have slopes whose products is p>0 Show that the locus of the points of intersection of the lines is a hyperbola.
View Solution
Knowledge Check
Two straight lines rotate about two fixed points (−a,0)and(a,o). If they start from their position of coincidence such that oen rotates at the rate double that of the other, then
The point(−a,0) always liesAinside the curveBoutside the curveCon the curveDnone of theseIf a line joining two points A(2,0),B(3,1) is rotated about A in anticlockwise direction through an angle 15∘ such that the point B goes to C in the new positon, then the coordinates of C are
A(2+1√2,√3)B(2+1√2,√32)C(2+1√2,√32)D(2−1√2,−√32)A line joining A(2,0) and B(3,1)is rotated about A .in anticlock wise direction through angle 150 ,then the equation of AB in the new position is
Ay−√2x+2√3=0By−√3x+√3=0Cy−√2x+√3=0Dy−√3x+2√3=0
If a line joining two points A(2,0) and B(3,1) is rotated about A in anti-clockwise direction 15∘, then the equation of the line in the new position is
View SolutionThe line 2x-y=3 is rotated through an angle π4 in anticlockwise direction about the point (2,1) ,then equation of line in its new position
View SolutionThe line 3x−4y+7=0 is rotated through an angle π4 in the clockwise direction about the point (−1,1). The equation of the line in its new position is
View SolutionThe line joining two points A(2,0) and B(3,1) is rotated about A in anticlockwise direction through an angle of 150 .If B goes to C in the new position,then the coordinates of C are
View SolutionThe point represented by the complex number 2−i is rotated about origin through on angle π2 the clockwise direction, the new position of the point is
View Solution
