Two tangents to the circle x2+y2=4 at the points A and B meet at P (- 4, 0). Then the area of the quadrilateral PAOB, O being the origin, is :Solution in Kannada
4
4√3
6√2
2√3
The correct Answer is:B
Step by step video, text & image solution for Two tangents to the circle x^2 + y^2 = 4 at the points A and B meet at P (- 4, 0). Then the area of the quadrilateral PAOB, O being the origin, is : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The term containing x3 in the expansion
(√x5+3√x3)6 appears in
View SolutionWhich one of the following is not correct for the features of exponential function given by f(x)=bx where b>1 ?
View SolutionTwo tangents to the circle x^(2)+y^(2)=4 at the points A and B meet at P(-4,0), The area of the quadrilateral PAOB, where O is the origin,is
View SolutionLet A be the centre of the circle x2+y2−2x−4y−20=0. Suppose that the tangent at the points B(1,7) and D(4,-2) on the circle meet at the point C. The area of the quadrilateral ABCD is
View Solutionआकृति में ,बाह्य बिंदु P से O केंद्र वाले वृत्त को PA एवं PB दो स्पर्श रेखाएं क्रमशः A व B पर स्पर्श करती है। सिद्ध कीजिए कि PAOB एक चक्रीय चतुर्भुज है।
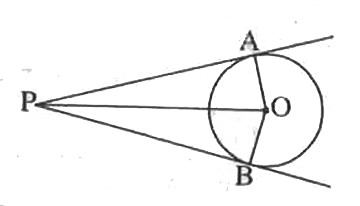
View SolutionLet A be the centre of the circle x2+y2−2x−4y−20=0. Let B(1,7) and (4,-2) be two points on the circle such that tangents at B and D meet at C. The area of the quadrilateral ABCD is
View Solutionमाना वृत्त x2+y2−2x−4y−20=0 का केन्द्र A है। माना वृत्त पर बिन्दु B(1,7) और D(4,−2) पर खींची गई स्पर्श रेखाएँ C पर मिलती है। चतुर्भुज ABCD का क्षेत्रफल है
View SolutionTwo tangents to the circle x2+y2=4 at the points A and B meet at P (- 4, 0). Then the area of the quadrilateral PAOB, O being the origin, is :
View SolutionFrom the point P(√2,√6) , tangents PAandPB are drawn to the circle x2+y2=4 Statement 1 :The area of quadrilateral OAPB(O being the origin) is 4. Statement 2 : The area of square is a2, where a is the length of side.
View SolutionLet A be the centre of the circle x2+y2−2x−4y−20=0 Suppose that the tangents at the points B(1,7) and D(4,-2) on the circle meet at the point C. Find the area of the quadrilateral ABCD
View Solutionमाना वृत्त x2+y2−2x−4y−20=0 का केन्द्र A है। माना वृत्त पर बिन्दु B(1,7) और D(4,−2) पर खींची गई स्पर्श रेखाएँ C पर मिलती है। चतुर्भुज ABCD का क्षेत्रफल है
View SolutionTwo tangents to the circle x2+y2=4 at the points A and B meet at point P(-4,0). The area of the quadrilateral PAOB in sq. units, where O is origin, is
View SolutionThe tangents at two points A and B on the circle with centre O intersect at P. If in quadrilateral PAOB, ∠AOB:∠APB=5:1, then measure of ∠APB is :
View SolutionIf the points of contact of the tangents drawn from an external points P to a circle with centre O be A and B,then show that PAOB is a cyclic quadrilateral.
View SolutionTangent are drawn from the point P(−1,5) to the circle x2+y2−4x−6y+4=0. If A and B be the points of contact of these tangents and ' O ' be the centre of the circle, then area of quadrilateral PAOB is
View Solutionमाना वृत्त x2+y2−2x−4y−20=0 का केन्द्र A है। माना वृत्त पर बिन्दु B(1,7) और D(4,−2) पर खींची गई स्पर्श रेखाएँ C पर मिलती है। चतुर्भुज ABCD का क्षेत्रफल है
View Solution
