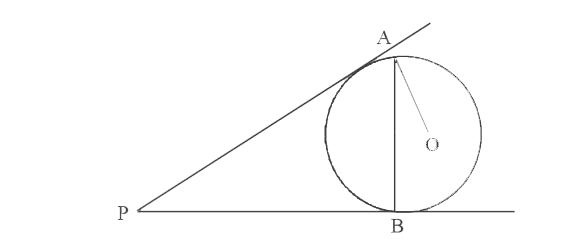
The tangents at two points A and B on the circle with centre O intersect at P. If in quadrilateral PAOB, ∠AOB:∠APB=5:1, then measure of ∠APB is :
30∘
60∘
45∘
15∘
The correct Answer is:A
To solve the problem step by step, we will follow the reasoning provided in the video transcript.
1. Understanding the Problem:
We have a circle with center O, and two tangents PA and PB drawn from an external point P. The angles we need to consider are ∠AOB and ∠APB, and we know the ratio of these angles is 5:1.
2. Setting Up the Angles:
Let ∠APB = k. According to the given ratio, ∠AOB = 5k.
3. Using the Properties of Tangents:
Since PA and PB are tangents to the circle at points A and B respectively, we know that:
- ∠PAO = 90° (the angle between the radius OA and the tangent PA)
- ∠PBO = 90° (the angle between the radius OB and the tangent PB)
4. Sum of Angles in Quadrilateral PAOB:
The sum of the angles in a quadrilateral is 360°. Therefore, we can write the equation:
∠PAO+∠PBO+∠APB+∠AOB=360°
Substituting the known values, we have:
90°+90°+k+5k=360°
5. Simplifying the Equation:
Combine like terms:
180°+6k=360°
6. Isolating k:
Subtract 180° from both sides:
6k=360°−180°
6k=180°
7. Solving for k:
Divide both sides by 6:
k=180°6=30°
8. Finding ∠APB:
Since ∠APB = k, we find:
∠APB=30°
Conclusion:
The measure of ∠APB is 30 degrees.
We have a circle with center O, and two tangents PA and PB drawn from an external point P. The angles we need to consider are ∠AOB and ∠APB, and we know the ratio of these angles is 5:1.
Let ∠APB = k. According to the given ratio, ∠AOB = 5k.
Since PA and PB are tangents to the circle at points A and B respectively, we know that:
- ∠PAO = 90° (the angle between the radius OA and the tangent PA)
- ∠PBO = 90° (the angle between the radius OB and the tangent PB)
The sum of the angles in a quadrilateral is 360°. Therefore, we can write the equation:
∠PAO+∠PBO+∠APB+∠AOB=360°
Substituting the known values, we have:
90°+90°+k+5k=360°
Combine like terms:
180°+6k=360°
Subtract 180° from both sides:
6k=360°−180°
6k=180°
Divide both sides by 6:
k=180°6=30°
Since ∠APB = k, we find:
∠APB=30°
The measure of ∠APB is 30 degrees.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The tangents at two points A and B on the circle with centre O Intersects at P, If in quadrilateral AOBP,∠AOB:∠APB=5:1, then measure of ∠APBis:
A30∘B60∘C45∘D15∘ - Question 2 - Select One
The tangents drawn at point A and B of a circle with centre O, meet at P. If ∠AOB=120∘ and AP = 6 cm, then what is the area of triangle APB (in cm2) ?
A6√3B8√3C9D9√3 - Question 3 - Select One
The tangents drawn at points A and B of a circle with centre O, meet at P. If ∠AOB=120∘ and AP=6cm then what is the area of quad APB (in cm2) ?
A6√3B8√3C9D12√3
In the circle with centre O and A,B,C are the points on the circle, ∠AOB=60∘. Find ∠ACB
 View Solution
View SolutionIf an equilateral triangle ABC is inscribed in a circle with centre O then the measure of ∠AOB is
View SolutionTwo circles with centres P and Q intersect at B and C, A, D are points on the circles with centres P and Q respectively such that A, C, D are colliner. If ∠APB=130∘,and∠BQD=x∘, then the value of x is :
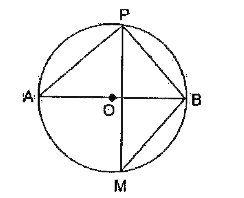
View SolutionIn the given figure, if AB is the diameter of the circle and PM the internal bisector of ∠APB, then the measure of angle ABM is
 View Solution
View SolutionFrom a point P two tangents PA and PB are drawn to a circle with centre O.if OP is equal to diameter of the circle then ∠APB is
View Solution