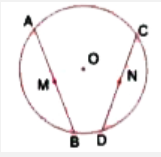
Two variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
The locus of the points of intersection of tangents at A and C is
x2+y2=a2
x2+y2=2a2
x2+y2=4a2
x2+y2=8a2
The correct Answer is:3
To find the locus of the points of intersection of the tangents at points A and C on the circle defined by the equation x2+y2=a2, we can follow these steps:
Step 1: Understand the Circle and Chords
The circle is defined by the equation x2+y2=a2. The chords AB and BC are of equal length a.
Step 2: Identify Midpoints
Let M and N be the midpoints of chords AB and BC, respectively. Since AB = BC = a, we can express the coordinates of points A, B, and C in terms of the angle subtended at the center.
Step 3: Parametrize Points A and C
Assume the coordinates of point A are (acosθ1,asinθ1) and point C are (acosθ2,asinθ2). The angle between the radius to A and C can be derived from the properties of the circle.
Step 4: Find the Midpoints M and N
The midpoints M and N can be calculated as:
- M=(acosθ1+acosθ22,asinθ1+asinθ22)
- N=(acosθ2+acosθ32,asinθ2+asinθ32)
Step 5: Equation of the Line MN
The line joining M and N can be expressed in a parametric form or slope-intercept form depending on the coordinates of M and N.
Step 6: Find Intersection Points P and Q
The line MN intersects the circle at points P and Q. We can substitute the equation of the line into the circle's equation to find these intersection points.
Step 7: Tangent at Points A and C
The equations of the tangents at points A and C can be derived using the point-slope form of the tangent to a circle. The tangent at point A is given by:
xcosθ1+ysinθ1=a
And similarly for point C:
xcosθ2+ysinθ2=a
Step 8: Intersection of Tangents
To find the locus of the intersection of the tangents at points A and C, we can solve the two equations simultaneously.
Step 9: Derive the Locus Equation
After solving the equations, we can derive the locus equation. The result will lead to the equation of a circle.
Final Step: Identify the Correct Option
From the derived locus equation, we can compare it with the given options:
1. x2+y2=a2
2. x2+y2=2a2
3. x2+y2=4a2
4. x2+y2=8a2
The correct answer is x2+y2=4a2.
The circle is defined by the equation x2+y2=a2. The chords AB and BC are of equal length a.
Let M and N be the midpoints of chords AB and BC, respectively. Since AB = BC = a, we can express the coordinates of points A, B, and C in terms of the angle subtended at the center.
Assume the coordinates of point A are (acosθ1,asinθ1) and point C are (acosθ2,asinθ2). The angle between the radius to A and C can be derived from the properties of the circle.
The midpoints M and N can be calculated as:
- M=(acosθ1+acosθ22,asinθ1+asinθ22)
- N=(acosθ2+acosθ32,asinθ2+asinθ32)
The line joining M and N can be expressed in a parametric form or slope-intercept form depending on the coordinates of M and N.
The line MN intersects the circle at points P and Q. We can substitute the equation of the line into the circle's equation to find these intersection points.
The equations of the tangents at points A and C can be derived using the point-slope form of the tangent to a circle. The tangent at point A is given by:
xcosθ1+ysinθ1=a
And similarly for point C:
xcosθ2+ysinθ2=a
To find the locus of the intersection of the tangents at points A and C, we can solve the two equations simultaneously.
After solving the equations, we can derive the locus equation. The result will lead to the equation of a circle.
From the derived locus equation, we can compare it with the given options:
1. x2+y2=a2
2. x2+y2=2a2
3. x2+y2=4a2
4. x2+y2=8a2
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - NUMERICAL VALUE TYPE
21 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - ARCHIVES (JEE MAIN)
1 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)
3 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
Two variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
∠OAB is
View SolutionTwo variable chords ABandBC of a circle x2+y2=r2 are such that AB=BC=r . Find the locus of the point of intersection of tangents at AandC.
View Solution
Knowledge Check
AB and CD are chords of the circle, and E and F are the midpoints of the chords, respectively. The line EF passes through the center O of the circle. IF EF=17. then what is radius of the circle?
 A10B12C13D15
A10B12C13D15
Two variable chords ABandBC of a circle x2+y2=r2 are such that AB=BC=r . Find the locus of the point of intersection of tangents at AandC.
View SolutionA chord AB of circle x2+y2=a2 touches the circle x2+y2−2ax=0.Locus of the point of intersection of tangens at A and B is :
View SolutionThe straight line x-2y+1=0 intersects the circle x2+y2=25 in points P and Q the coordinates of the point of intersection of tangents drawn at P and Q to the circle is
View SolutionThe straight line x−2y+5=0 intersects the circle x2+y2=25 in points P and Q, the coordinates of the point of the intersection of tangents drawn at P and Q to the circle is
View SolutionIn the figure, O is the center of the circle and BO is the bisector of ∠ABC show that AB=BC
View SolutionAB and AC are two chords of a circle of radius r such that AB=2AC. If p and q are the distances of AB and AC from the centre Prove that 4q2=p2+3r2.
View SolutionM and N are the mid-points of two equal chords AB and CD respectively of a circle with centre O. Prove that :
∠AMN=∠CNM.
View Solution
