Use the principle of mathematical induction to show that 52n+1+3n+2.2n−1 divisible by 19 for all natural numbers n.Solution in Punjabi
Let P(n)=52n+1+3n+2.2n−1
Step I For n=1,P(1)=52+1+31+2.21−1=125+27=152, which is divisible by 19.
Step II Assume that the result is true for n=k, i.e.,
P(k)=52k+1+3k+2.2k−1 is divisible by 19.
⇒P(k)=19r, where r is an integer .
Step III for n=k+1.
P(k+1)=52(k+1)+1+3k+1+2.2k+1−1
52k+3+3k+3.2k
=25.52k+1+3.3k+2.2.2k−1
=25.52k+1+6.3k+2.2k−1
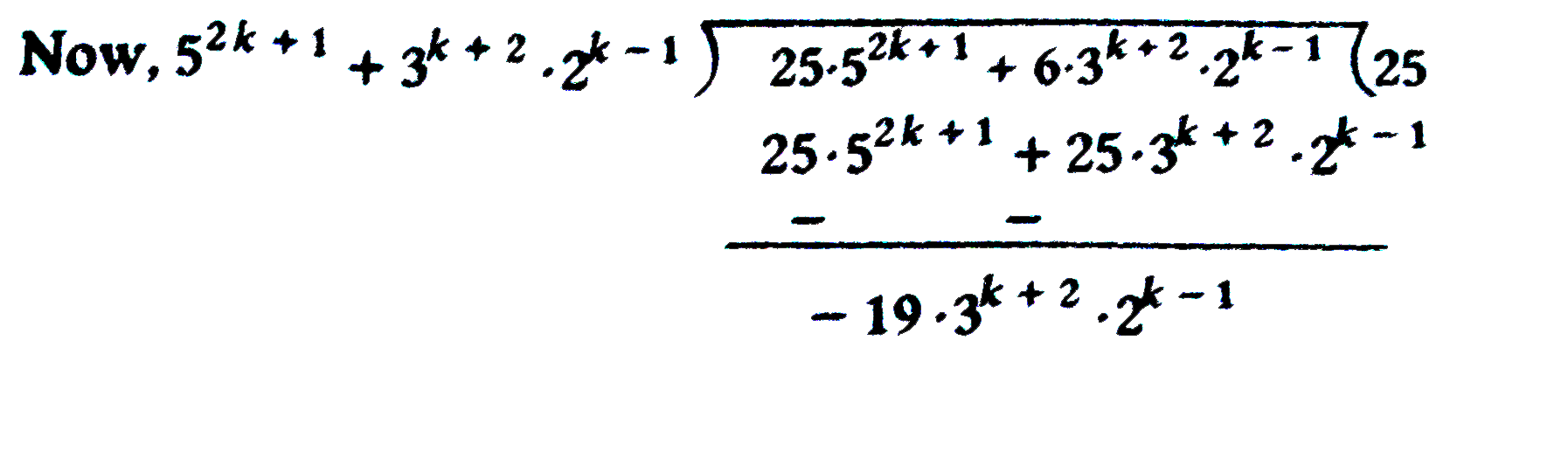
∴25.56(2k+1)+6.3k+2.2k−1=25.(52k+1+3k−2.2k−2)−19.3k+2.2k−1
i.e., P(k+1)=25P(k)−19.3k+2.2k−1
But we know that P(k) is divisible by 19. Also , 19.3k+2.2k−1 is clearly divisible by 19.
Therefore , P(k+1) is divisible by 19. This shows that the result is true for n=k+1.
Hence , by the principle of mathematical induction , the result is true for all n∈N.
Topper's Solved these Questions
- MATHEMATICAL INDUCTION BOOK - ARIHANT MATHSCHAPTER - MATHEMATICAL INDUCTION EXERCISE - Mathematical Induction Exercise 1: (Single Option Correct Tpye Questions)
3 Videos
- MATHEMATICAL INDUCTION BOOK - ARIHANT MATHSCHAPTER - MATHEMATICAL INDUCTION EXERCISE - Exercise (Statement I And Ii Type Questions)
3 Videos
- LOGARITHM AND THEIR PROPERTIESBOOK - ARIHANT MATHSCHAPTER - LOGARITHM AND THEIR PROPERTIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
4 Videos
- MATRICES BOOK - ARIHANT MATHSCHAPTER - MATRICES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
49 Videos
Similar Questions
If an=√7+√7+√7+.......) having n radical signs then by methods of mathematical induction which is true
View SolutionIf a1=1,a2=5 find the common difference and 5th term of A.P
View SolutionIn Which quadrant Point (−2,−3) will be lie.
View SolutionLet A=⎡⎢⎣1000110−24⎤⎥⎦,I=⎡⎢⎣100010001⎤⎥⎦andA−1=[16(A2+cA+dI)] Then value of candd are (a) (−6,−11) (b) (6,11) (c) (−6,11) (d) (6,−11)
View SolutionUsing the Principle of mathematical induction, show that 11n+2+122n−1, where n is a naturla number is a natural number is divisible by 133.
View SolutionUsing principle of mathematical induction, prove that 74n−1 is divisible by 22n+3 for any natural number n.
View SolutionShow by using the principle of mathematical induction that for all natural number n>2,2n>2n+1
View SolutionUsing the principle of Mathematical Induction, show that 2.42n+1+33n+1 is divisible by 11, ∀n∈N
View SolutionProve by principle of Mathematical Induction that for all natural number in n(n+1)(n+2) is divisible by 6.
View SolutionUsing principle of mathematical induction, prove that 74n−1 is divisible by 22n+3 for any natural number n.
View SolutionProve the following by using the principle of mathematical induction for all n∈N
(2n+1)<2n,n≥3
View SolutionProve the statement by the principle of mathematical induction :
32n−1 is divisible by 8, for all natural number n.
View SolutionProve by the principle of mathematical induction that for all n in N.(102n−1+1) is divisible by 11 for all n∈N.
View SolutionProve by the principle of mathematical induction that for all n in N.52n−1 is divisible by 24 for all n∈N.
View SolutionUsing the principle of mathematical induction prove that 32n+1+2n+2is divisible by 7[n∈N]
View SolutionShow by using the principle of mathematical induction that for all natural number n>2,2n>2n+1
View Solution
