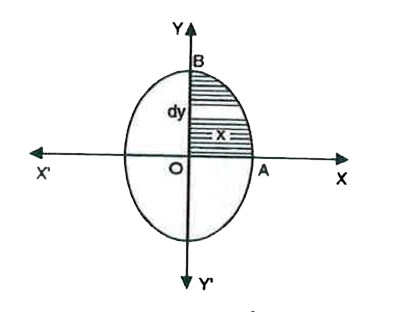
Using definite integration, find the area of the smaller region bounded by the ellipse $9 x^{2} + 16 y^{2} = 144 and x = 2 .$

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $(4 π - 3 \sqrt{3})$ sq. units.

|

Answer

Step by step video, text & image solution for Using definite integration, find the area of the smaller region bounded by the ellipse 9x^2 + 16 y^2 = 144 and x =2. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Find the area of the region bounded by the ellipse $\frac{x^{2}}{4} + \frac{y^{2}}{9} = 1 .$

A $10 π$
B $11 π$
C $12 π$
D $13 π$
Question 2 - Select One
Find the area of the region bounded by the ellipse $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ in fourth quadrant.
A $\frac{3 π}{4}$ sq units
B $\frac{3 π}{2}$ sq units
C $\frac{5 π}{2}$ sq units
DNone of these
Question 3 - Select One
The area of the region bounded by the ellipse $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$ is
A $20 π sq units$
B $20 π^{2} sq units$
C $16 π^{2} sq units$
D $25 π sq units$

NAGEEN PRAKASHAN-APPLICATIONS OF INTEGRALS-Exercise 8a

Home
Ask Doubt
Profile