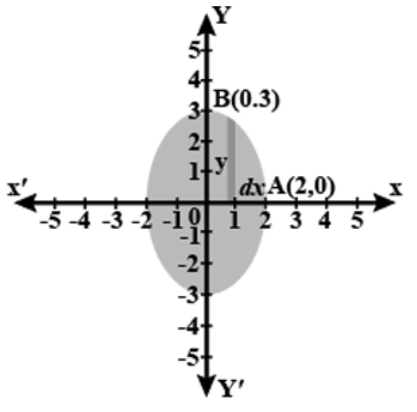
Find the area of the region bounded by the ellipse $\frac{x^{2}}{4} + \frac{y^{2}}{9} = 1$

Video Solution

Text Solution

Verified by Experts

The given equation of the ellipse can be represented as $\frac{x^{2}}{4} + \frac{y^{2}}{9} = 1$
the standard form of ellipse is given by $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$
by comparing we get,
$a = 2$ and $b = 3$
$\Rightarrow y = 3 \sqrt{1 - \frac{x^{4}}{4}} ... ... (i)$
It can be observed that the ellipse is symmetrical about x-axis and y-axis.
Area bounded by ellipse = $4 \times$ Area $O A B$
now
Area of $O A B$ $= \int_{0}^{a} y d x = \int_{0}^{2} y d x$
$= \int_{0}^{2} 3 \sqrt{1 - \frac{x^{4}}{4}} d x$
$= \frac{3}{2} \int_{0}^{2} \sqrt{4 - x^{2}}$ dx
$= \frac{3}{2} {[\frac{x}{2} . \sqrt{4 - x^{2}} + \frac{4}{2} {sin}^{- 1} (\frac{x}{2})]}_{0}^{2}$
$= \frac{3}{2} [\frac{2 π}{2}] = \frac{3 π}{2}$
Therefore, area bounded by the ellipse $= 4 \times \frac{3 π}{2} = 6 π$ sq. units

Updated on:21/07/2023

Find the area of the region bounded by the ellipse $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ in fourth quadrant.
A $\frac{3 π}{4}$ sq unit
B $\frac{3 π}{2}$ sq unit
C $\frac{9 π}{4}$ sq unit
D $\frac{4 π}{7}$ sq unit
Find the area of the region bounded by the ellipse $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ in fourth quadrant.
A $\frac{3 π}{4}$ sq units
B $\frac{3 π}{2}$ sq units
C $\frac{5 π}{2}$ sq units
DNone of these
The area of the region bounded by the ellipse $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$ is
A $20 π sq units$
B $20 π^{2} sq units$
C $16 π^{2} sq units$
D $25 π sq units$