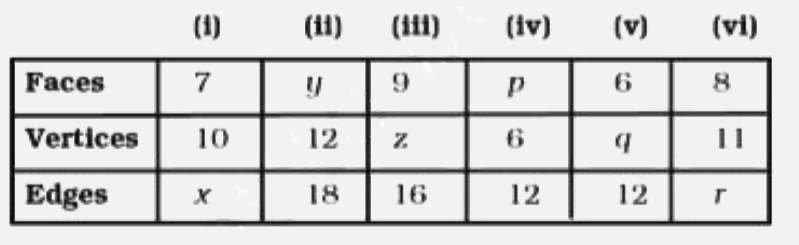
Using Euler's formula, find the value of P, Q and R respectively.
Faces : P, 5, 20
Vertices : 6, Q, 12
Edges : 12, 9, R
7, 5, 25
8, 6, 30
12, 9, 21
20, 2, 18
The correct Answer is:B
To solve the problem using Euler's formula, we will follow these steps:
Step 1: Understand Euler's Formula
Euler's formula states that for any convex polyhedron, the relationship between the number of faces (F), vertices (V), and edges (E) is given by:
F+V−E=2
Step 2: Set Up the Equations
We have the following information:
- Faces: F=P,5,20
- Vertices: V=6,Q,12
- Edges: E=12,9,R
We will create three equations based on Euler's formula for each set of values.
Step 3: Solve for P
Using the first set of values:
- F=P
- V=6
- E=12
Substituting into Euler's formula:
P+6−12=2
Now, simplify:
P−6=2
P=2+6
P=8
Step 4: Solve for Q
Using the second set of values:
- F=5
- V=Q
- E=9
Substituting into Euler's formula:
5+Q−9=2
Now, simplify:
Q−4=2
Q=2+4
Q=6
Step 5: Solve for R
Using the third set of values:
- F=20
- V=12
- E=R
Substituting into Euler's formula:
20+12−R=2
Now, simplify:
32−R=2
−R=2−32
−R=−30
R=30
Final Values
We have found:
- P=8
- Q=6
- R=30
Conclusion
Thus, the values of P,Q, and R are 8,6, and 30 respectively.
---
Euler's formula states that for any convex polyhedron, the relationship between the number of faces (F), vertices (V), and edges (E) is given by:
F+V−E=2
We have the following information:
- Faces: F=P,5,20
- Vertices: V=6,Q,12
- Edges: E=12,9,R
Using the first set of values:
- F=P
- V=6
- E=12
P+6−12=2
P−6=2
P=2+6
P=8
Using the second set of values:
- F=5
- V=Q
- E=9
5+Q−9=2
Q−4=2
Q=2+4
Q=6
Using the third set of values:
- F=20
- V=12
- E=R
20+12−R=2
32−R=2
−R=2−32
−R=−30
R=30
We have found:
- P=8
- Q=6
- R=30
Thus, the values of P,Q, and R are 8,6, and 30 respectively.
Topper's Solved these Questions
- IMO MODEL TEST PAPER -3BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO MODEL TEST PAPER -3EXERCISE - Everyday Mathematics
10 Videos
- IMO MODEL TEST PAPER -3BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO MODEL TEST PAPER -3EXERCISE - Achievers Section
5 Videos
- IMO MODEL TEST PAPER -3BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO MODEL TEST PAPER -3EXERCISE - Achievers Section
5 Videos
- IMO MODEL TEST PAPER 1BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO MODEL TEST PAPER 1EXERCISE - ACHIEVERS SECTION
5 Videos
Similar Questions
Knowledge Check
If p→(q∧r) is false, then the truth values of p,q and r are respectively
AT,F and FBF,F and FCF, T and TDT,T and FIf p→q(q∨r) is false, then the truth values of p,q,r are respectively
AT,F,FBF,F,FCF,T,TDT,T,FIf P varies directly as QR and the values of P, Q. R be 6, 9, 10 repectively, then the value of P when Q = 5 and R= 3 is
A12B3C13D1
Using Euler’s formula find the unknown.
Faces ?,5,20 ,
vectices 6,?,12
Edges 12,9,?
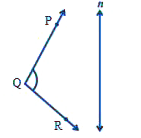
View SolutionDraw the images P' , Q' and R' of the point P, Q and R respectively in the line n (Fig . 9. 18). Join P' Q' and Q' R' to form an angle P' Q' R' Measure ∠PQRand∠P'Q'R' . Are the two angles equal ?
View SolutionUsing integration, find the area of the triangle PQR, coordinates of whose vertices are P(2, 0), Q(4, 5) and R(6, 3).
View SolutionThe ratio of the speed of P, Q and R is 10:12:15 respectively. What is the ratio of the time taken by P. Q and R respectively to cover the same distance?
View SolutionThe ratio of the speed of P, Q and R is 10:12:15 respectively. What is the ratio of the time taken by P. Q and R respectively to cover the same distance?
View Solution