Using integration, find the area of the region bounded by the triangle ABC whose vertices A, B, C are (-1, 1), (0,5) and (3,2) respectively.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:N/a

Let we have the vertices of a $Δ A B C as A (- 1, 1), B (0, 5) as A (- 1, 1), B (0, 5) and (3, 2)$ .

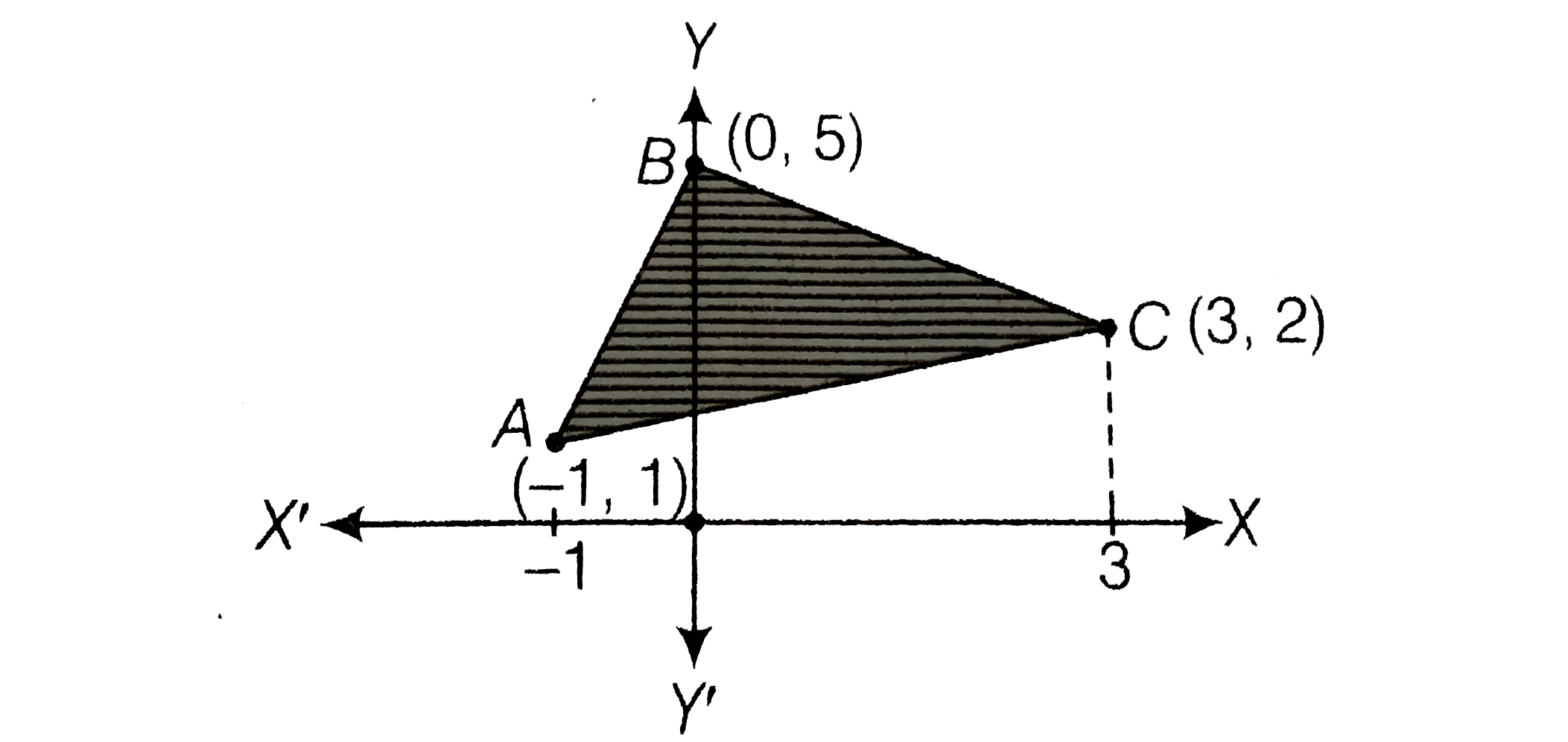
$∴ Equation of AB is y - 1 = (\frac{5 - 1}{0 + 1}) (x + 1)$
$\Rightarrow y - 1 = 4 x + 4$
rArr y=4x+5 â€¦(i)
and equation of BC is $y - 5 = (\frac{2 - 5}{3 - 0}) (x - 0)$
$\Rightarrow y - 5 = \frac{- 3}{3} (x)$
$\Rightarrow y = 5 - x$
Similarly, equation of AC is $y - 1 = (\frac{2 - 1}{3 + 1}) (x + 1)$
$\Rightarrow y - 1 = \frac{1}{4} (x + 1)$
$\Rightarrow 4 y = x + 5$
$∴ Area of shaded region = \int_{- 1}^{0} (y_{1} - y_{2}) d x + \int_{0}^{3} (y_{1} - y_{2}) d x$
$= \int_{- 1}^{9} [4 x + 5 - \frac{x - 5}{4}] d x + \int_{0}^{3} [5 - x - \frac{x + 5}{4}] d x$
$= {[\frac{4 x^{2}}{2} + 5 x - \frac{x^{2}}{8} - \frac{5 x}{4}]}_{- 1}^{0} + {[5 x - \frac{x^{2}}{2} - \frac{x^{2}}{8} - \frac{5 x}{4}]}_{0}^{3}$
$= [0 - (4 . \frac{1}{2} + 5 (- 1) - \frac{1}{8} + \frac{5}{4})] + [(15 - \frac{9}{2} - \frac{9}{8} - \frac{15}{4}) - 0]$
$= [- 2 + 5 - \frac{1}{8} - \frac{5}{4} + 15 - \frac{9}{2} - \frac{9}{8} - \frac{15}{4}]$
$= 18 + (\frac{1 - 10 - 36 - 9 - 30}{8})$
$= 18 + (- \frac{84}{8}) = 18 - \frac{21}{2} = \frac{15}{2} sq units$

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

NCERT EXEMPLAR ENGLISH-APPLICATION OF INTEGRALS-Long Answer Type Questions

Home
Ask Doubt
Profile