Using integration find the area of the triangular region whose sides have equations $y = 2 x + 1, y = 3 x + 1$ and $x = 4$

Video Solution

Text Solution

Verified by Experts

Equation of the sides of $△ A B C$ ,
Let equation of AB is $y = 2 x + 1$
Equation of BC is $y = 3 x + 1$
Equation of AC is $x = 4$

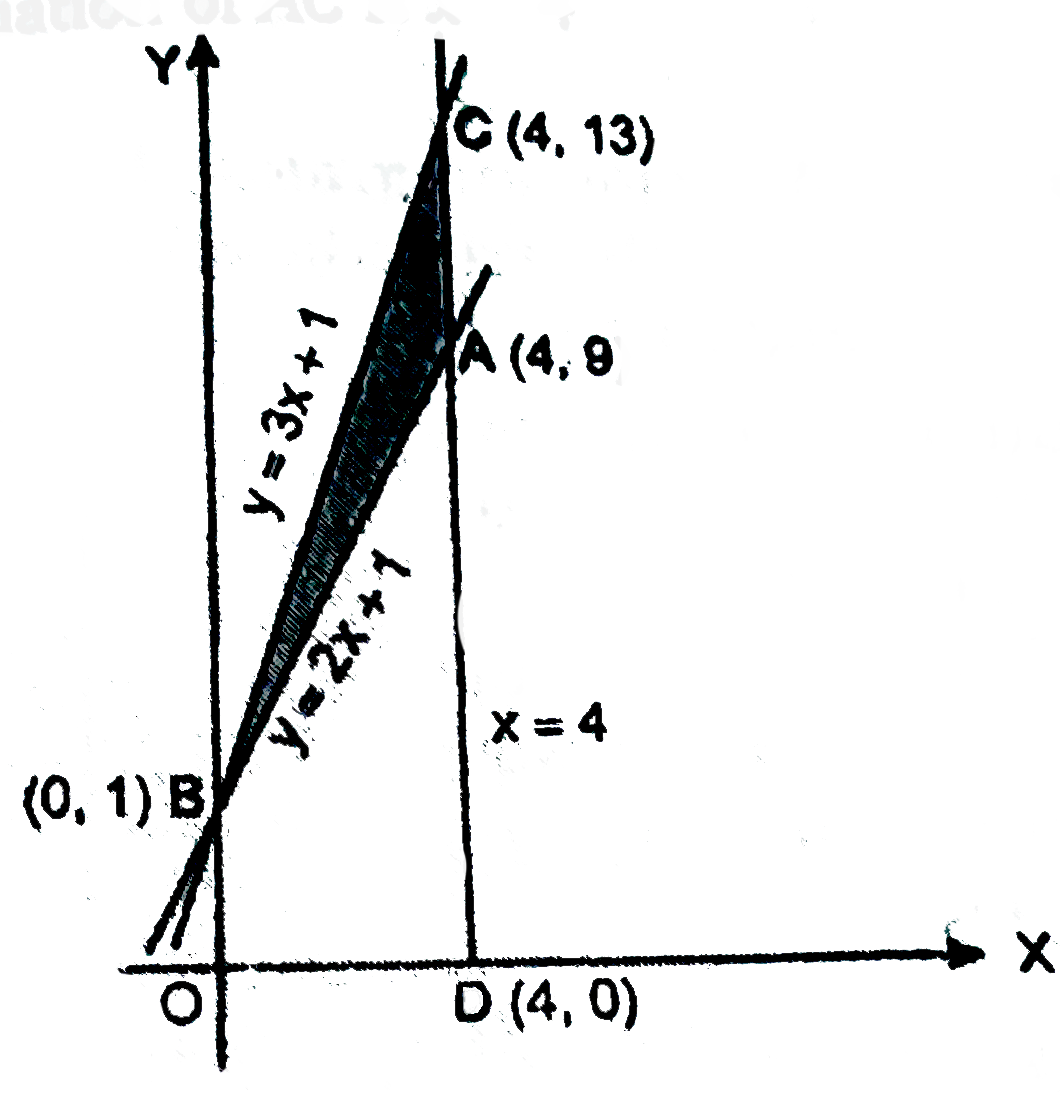
Their points of intersection i.e, coordinates of A, B and C respectively are (4, 9), (0, 1) and (4, 13).
Now $a r (△ A B C)$
$= a r (△ (O D C B O) - a r (O D A B O)$
$= \int_{0}^{4} (3 x + 1) d x - \int_{0}^{4} (2 x + 1) d x$
$= \int_{0}^{4} x d x = {[\frac{x^{2}}{2}]}_{0}^{4} = 8$ sq. units.

Find the orthocentre of the triangle whose sides have the equations y = 15, 3x = 4y, and 5x + 12y = 0.
A(0, 0)
B(0, -33)
C(- 33, 33)
D(- 33, 0)
Find the area of the triangle formed by the straight lines whose equations are 2y+x−5=0,y+2x−7=0, and x−y+1=0.
Aa. $\frac{3}{2}$
Bb. 10
Cc. 6
Dd. $\frac{2}{5}$
Find the area of the triangle formed by the straight lines whose equations are 2y+x−5=0,y+2x−7=0, and x−y+1=0.
A $\frac{3}{10}$
B10
C6
D $\frac{2}{5}$