Using integration find the area of the triangular region whose sides have equations y=2x+1, y=3x+1 and x=4
Equation of the sides of △ABC,
Let equation of AB is y=2x+1
Equation of BC is y=3x+1
Equation of AC is x=4
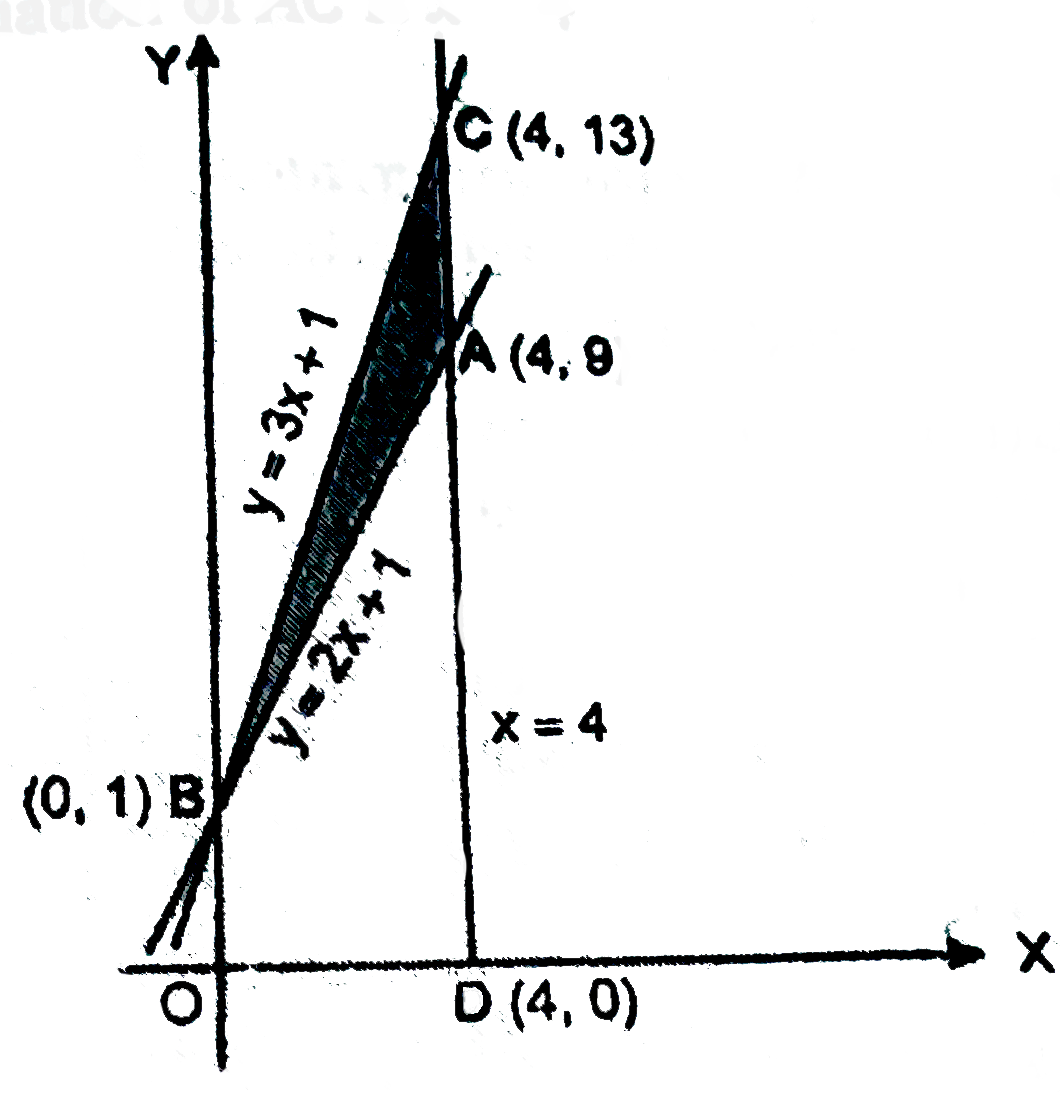
Their points of intersection i.e, coordinates of A, B and C respectively are (4, 9), (0, 1) and (4, 13).
Now ar(△ABC)
=ar(△(ODCBO)−ar(ODABO)
=∫40(3x+1)dx−∫40(2x+1)dx
=∫40xdx=[x22]40=8 sq. units.
Topper's Solved these Questions
- APPLICATIONS OF INTEGRALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Miscellaneous Exercise
19 Videos
- APPLICATIONS OF INTEGRALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Exercise 8.1
13 Videos
- APPLICATIONS OF DERIVATIVESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Miscellaneous Exercise
24 Videos
- Continuity and DifferentiabilityBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - Continuity and DifferentiabilityEXERCISE - Miscellaneous Exercise
23 Videos
Similar Questions
Find the area of the triangular region bounded by the sides y=2x+1,y=3x+1andx=4
View SolutionFind the vertices and the area of the triangle whose sides are x=y,y=2xandy=3x+4.
View SolutionSketch the graph of y=|x+4|. Using integration find the area of the region bounded by the curve y=|x+4| and x= -6 and x=0.
View SolutionUsing integration, find the area of the following region: R={(x,y):x2≤y≤|x|}
View SolutionUsing definite integration, find the area of the smaller region bounded by the ellipse 9x2+16y2=144andx=2.
View SolutionUsing integration, find the area of the region bounded by the curves y=x and y=x3.
View SolutionFind the area of the triangular region bonded by x= 0, y = x and x + 2y =6
View SolutionUsing intergration, find the area of the region bounded by the lines y=|x+1|,x=−3,x=1 and X-axis.
View SolutionUsing integration, find the area of the region bounded by the lines y=1+|x+1|,x=−2,x=3andy=0.
View SolutionFind the graphically, the vertices of the triangle whose sides have the equations 2y−x=8,5y−x=14 and y−2x=1 respectively.
Take 1 cm=1 unit on both the axes.
View Solution
