Using suitable identity, prove that :
(0.67)3+(0.33)3(0.67)2−(0.67×0.33)+(0.33)2=1
To prove the given expression
(0.67)3+(0.33)3(0.67)2−(0.67×0.33)+(0.33)2=1,
we will use the identity for the sum of cubes and the algebraic manipulation of the denominator.
1. Identify Variables: Let a=0.67 and b=0.33.
2. Use the Sum of Cubes Identity: Recall the identity for the sum of cubes:
a3+b3=(a+b)(a2−ab+b2).
Thus, we can rewrite the numerator:
a3+b3=(a+b)(a2−ab+b2).
3. Substitute into the Expression: Substitute this identity into the expression:
a3+b3a2−ab+b2=(a+b)(a2−ab+b2)a2−ab+b2.
4. Cancel the Common Terms: The a2−ab+b2 in the numerator and denominator cancels out, provided a2−ab+b2≠0:
=a+b.
5. Calculate a+b: Now substitute back the values of a and b:
a+b=0.67+0.33=1.
6. Conclusion: Therefore, we have shown that:
(0.67)3+(0.33)3(0.67)2−(0.67×0.33)+(0.33)2=1.
Final Result:
Hence, the expression is proved to be equal to 1.
---
a3+b3=(a+b)(a2−ab+b2).
Thus, we can rewrite the numerator:
a3+b3=(a+b)(a2−ab+b2).
a3+b3a2−ab+b2=(a+b)(a2−ab+b2)a2−ab+b2.
=a+b.
a+b=0.67+0.33=1.
(0.67)3+(0.33)3(0.67)2−(0.67×0.33)+(0.33)2=1.
Hence, the expression is proved to be equal to 1.
Topper's Solved these Questions
- FOOTSTEPS TOWARDS CBSE BOARDBOOK - MTG IIT JEE FOUNDATIONCHAPTER - FOOTSTEPS TOWARDS CBSE BOARDEXERCISE - PART-B (SECTION-IV)
4 Videos
- FOOTSTEPS TOWARDS CBSE BOARDBOOK - MTG IIT JEE FOUNDATIONCHAPTER - FOOTSTEPS TOWARDS CBSE BOARDEXERCISE - PART-A (SECTION-II)
16 Videos
- FOOTSTEPS TOWARDS (JEE MAIN)BOOK - MTG IIT JEE FOUNDATIONCHAPTER - FOOTSTEPS TOWARDS (JEE MAIN)EXERCISE - Section B (Numerical Value Type Questions)
10 Videos
- HERON'S FORMULABOOK - MTG IIT JEE FOUNDATIONCHAPTER - HERON'S FORMULAEXERCISE - OLYMPIAD/HOTS CORNER
7 Videos
Similar Questions
Knowledge Check
The value of (0.67×0.67×0.67)−(0.33×0.33×0.33)(0.67×0.67)+(0.67×0.33)+(0.33×0.33) is
A11B1.1C3.4D0.34Find the sum of 0.30.5+0.330.55+0.3330.555+… to 15 terms.
A10B9C3D5Which of the following is the correct option
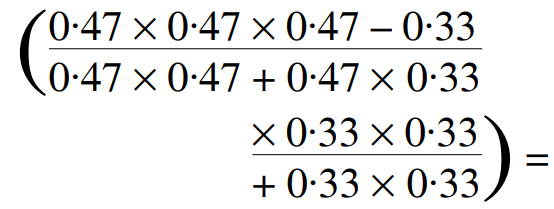 A0.14B0.8C15.51D1
A0.14B0.8C15.51D1
Using logarithmic tables, evaluate:
5.670.304×45.42
View Solution0.34¯¯¯¯67+0.13¯¯¯¯33
View Solution(0.34¯¯¯¯67+0.13¯¯¯¯33) का मान है।
View SolutionThe initial and final temperature of a liquid are measured to be (67.7±0.2)0c and (76.3±0.3)0c then rise in temperture with error limit is
View Solution(0.22)3+(0.11)3+(0.32)3(0.66)3+(0.96)3+(0.33)3+(0.32)3+(0.45)3−(0.77)381(0.32)(0.45)(0.77) equals
View Solution
