Using the digits 1, 2, 3, 4, 5, 6,7, a number of 4 different digits is formed. Find

Video Solution

Text Solution

Verified by Experts

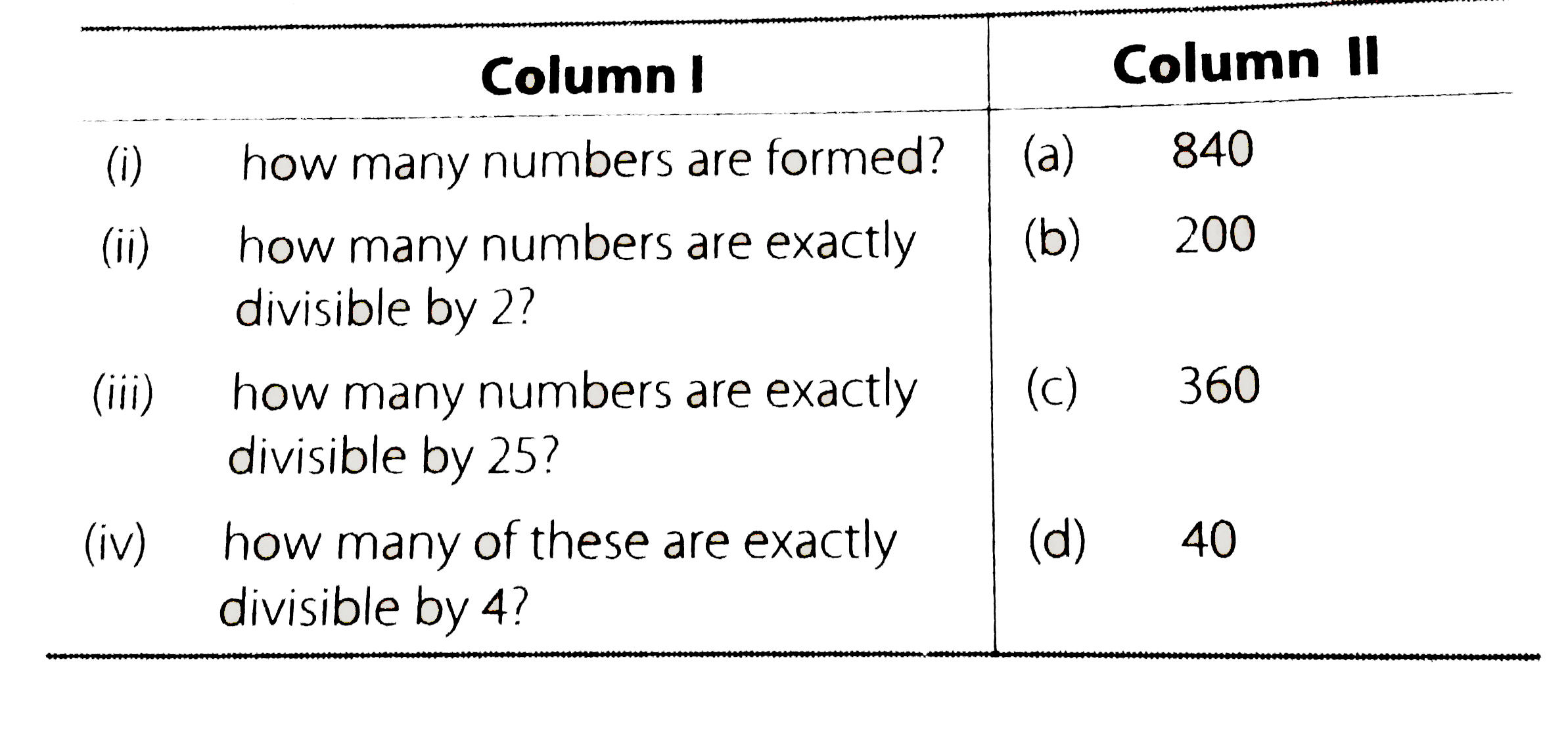
(i) Total number of 4 digit formed with digit 1, 2, 3, 4, 5, 6, 7
$= 7 \times 6 \times 5 \times 4 = 840$
(ii) When a number is divisible by 2. At its unit place only even numbers occurs.
Total numbers $= 4 \times 5 \times 6 \times 3 = 360$
(iii) Total numbers which are divisible by 25 = 40
(iv) A number is divisible 4, If its last two digit is divisible by 4.
$∴$ Total such numbers = 200

|

Updated on:21/07/2023

Class 11 MATHS PERMUTATIONS AND COMBINATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The number of five-digit numbers which are divisible by $3$ that can be formed by using the digits $1, 2, 3, 4, 5, 6, 7, 8$ and $9$ , when repetition of digits is allowed, is
A $3^{9}$
B ${4.3}^{8}$
C ${5.3}^{8}$
D ${7.3}^{8}$
Question 2 - Select One
A four digit number of distinct digits is formed by using the digits 2, 3, 4, 5, 6, 7, 8. The number of such numbers which are divisible by 25, is
A60
B40
C20
D15
Question 3 - Select One
How many even numbers of 3 different digits can be formed from the digits 1, 2, 3, 4, 5, 6, 7, 8, 9 (repetition of digits is not allowed) ?
A224
B280
C324
DNone of these

NCERT EXEMPLAR-PERMUTATIONS AND COMBINATIONS-Matching The Columns

Home
Ask Doubt
Profile