Volume of pyramid
Volume of Pyramid
In this chapter, we will study volume of pyramid. We will also learn the formula for volume of pyramid as well as the pyramid triangle. You would also be able to work on some examples where it would lead to getting the right and clear idea of it. It is important to note that the volume of pyramid is dependent on the type of the base of the pyramid. So, it depends on whether the base is a square, triangle or rectangle. It proves to be a poly sided figure when it comes to the base of the pyramid. So, it is on the basis of the structure of the height and the base of the pyramid that is required for the formula to find out its volume and also its surface area. Let us go ahead and learn more about it in the best way.
The derivation of Volume of a Pyramid
It is quite important to get the right knowledge of the total capacity of the given pyramid when you need to find the volume of a pyramid. Coming to the formula for the volume of a pyramid, it is given as :
Volume = 1/3 x Area of the Base x Height or
V = (1/3) A x H
Here, A = Area, H = height and V = Volume
It is the following units that the volume of a pyramid is measured
It’s volume is measured in the following units:
- ft3
- in3
- cm3
- m3 etc
While calculating the volume, it is always important to keep all the measurement units the same. We will study the formula for the different types of pyramids.
Formula for Volume of Pyramid
Volume of Triangular Pyramid
There is a triangular base in this type of pyramid. We know that the area of a triangle is
A= ½ b x h, be is the base and ‘h’ is the height of triangle.
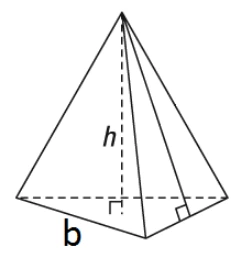
So, when it comes to the volume of a triangular pyramid;
V = 1/3 x Area of base x Height of pyramid
V = 1/3 x (1/2 b.h) x H
V = 1/6 bhH
Volume of Rectangular Pyramid
There is a presence of a base in the shape of a rectangle in a rectangular pyramid. The product of its length and width is the area of the rectangle where,
A = Length x Width
A = lw
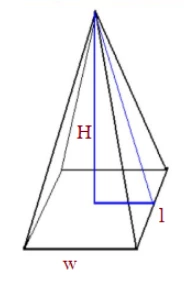
So, when it comes to the volume of a rectangular pyramid, it is given by:
V = 1/3 x A x H
V = 1/3 lwH
Volume of Square Pyramid
When it comes to the square-based pyramid, it has a square base. We are familiar that the area of a square is given by;
A = a2, Here, the length of the side of the square is ‘a’.
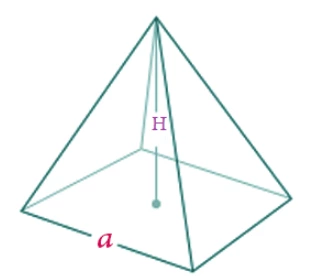
So, coming to the volume of a square-sided pyramid, it is;
V = 1/3 x Area of square base x Height
V = 1/3 x a2 x H
V = 1/3 a2 H
Volume of Hexagonal Pyramid
When it comes to the volume of a hexagonal pyramid, it has got the base in a regular hexagon shape which is given by:
Volume = 1/3 x area of base x height
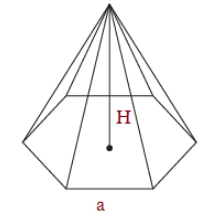
V= 1/3 x 3√3/2 a2 x H
V = √3/2 a2 H
Here ‘a’ is the side length of the hexagon base, whereas H is the height of the pyramid.
Related Videos:
- Surface area of pyramid
- Volume of a cube
- Volume of a cuboid
- Volume and surface area of cone
- Volume of Sphere and Hemisphere
We will now concentrate on some examples to get a clear idea on how to solve different questions:
Problem 1: The base of a pyramid is square in shape. When it comes to the sides of the base, they are 10 cm each where the height of the pyramid is 21cm. Can you find out the volume of the pyramid?
Solution: To find the volume of a pyramid, we will use the formula – V = ⅓ A H
According to the question, the base of the pyramid is a square. Here, will find the area of the base, which is:
a2 = 10 x 10 = 100 cm2
= ⅓ x 100 cm 2 x 21 cm
= 100 x 7
= 700 cm3
Therefore the volume of the pyramid is 700 cm3.
Problem 2: The base of a pyramid is square in shape. The sides of the base are 14 cm each, and the height is 21cm. Can you find the volume of the pyramid?
Solution: When it comes to finding the volume of a pyramid, we make use of the formula – V = ⅓ A H
It is given that the base of the pyramid is a square. Here, the area of the base is
a2 = 14 x 14 = 196cm2
= ⅓ x 196 cm 2 x 21 cm
= 196 x 7
= 1102 cm3
Therefore the volume of the pyramid is 1102 cm3.
Problem 3: The base of the pyramid is rectangular in shape. It has got a length of 9 cm, and the width is 7 cm, and the height of the pyramid is 10cm. Can you find its volume?
Solution: Given, the length of rectangular base of pyramid = 9 cm
width = 7 cm
and height of the pyramid = 10cm
We know, the volume of rectangular pyramid,
V = 1/3 l w H
Substituting the values we get;
V = 1/3 x 9 x 7 x 10
V = 630/3 = 210 cm3
Therefore the volume of the pyramid is 210 cm3.
Problem 4: The area of the base of a triangular pyramid is 165 cubic cm. The height is 7 cm. Can you find its volume?
Solution: Given the area of the base of pyramid = 165 cu.cm
We know that
Volume of pyramid = 1/3 x A x H
So, V = 1/3 x 165 x 7
V = 55 x 7
V = 385 cm3.
Important Chapters:




Similar Questions
Knowledge Check
The volume a pyramid of base area 25cm2 and height 12 cm is :
A200cm3B100cm3C400cm3D800cm3The volume a pyramid of base area 25cm2 and height 12 cm is :
A200cm3B100cm3C400cm3D800cm3The base area of a right pyramid is 57 sq. units and height is 10 units. Then the volume of the pyramid is
A190 cubic unitsB380 cubic unitsC540 cubic unitsD570 cubic units
A and B are the volumes of a pyramid and a right prism respectively. If the pyramid and the prism have the same base area and the same height, then what is the relation between A and B?
View SolutionA regular square based pyramid is inscribed in a sphere of given radius R so that all vertices of the pyramid belong to the sphere. Find the greatest value of the volume of the pyramid.
View SolutionThe base of a right pyramid is a square of side 40 cm long. If the volume of the pyramid is 8000cm3, then its height is :
View SolutionA right pyramid 6m height has a square base of which the diagonal is √1152m. Volume of the pyramid is
View SolutionThe base of a right pyramid is an equilateral triangle of perimeter 8 dm and the height of the pyramid is 30√3 cm. Find the volume of the pyramid.
View Solution
