What is function ?
What is a Function?
If every element of a non-void set X has a single image or range to a non-void set Y in a relation ‘f’, then relation ‘f’ is called a function.
Or
If ‘f’ is a function from set X to set Y and (x,y) ∊ f, then f(x) = y, where a has an image as b, under function f and b has a preimage as a, under ‘f’. It is denoted as;
f: X → Y.
Example: N be a set of all the Natural numbers, and the relation F be defined as;
F = {(x,y) : y=x2, x,y ∈ N}. State either F is a relation function or not.
Solution: From the relation F= {(x,y): y=x2, a,b ∈ N}, it can be seen that for every value of a natural number, there is a single image. Like if x=1 then y =1 if x=2 then y=4 and so on. Hence, F is a relation function in this case.
To learn about the Domain and Range of a relation, let us know what relations are.
Relations:
To know what relations are, we should initially know about the Cartesian product. A group of all the ordered pairs (x,y) is called the cartesian product where x ∈ X and y ∈ Y. A subset of a cartesian product is called a relation. Generally, a relation is a rule that “connects” an element from one set to an element of another set.
Definition: A relation R is specified as a subgroup(subset) of cartesian product A×B. Here A and B are two non-void sets.
This subset is the result of the “connection” specified among the elements of the first and the second set.
R= {(p,q):p ∈ A and q ∈ B}
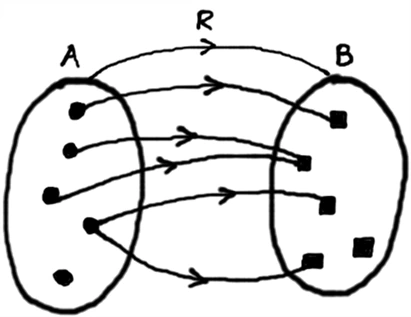
In figure 1, a relation from set A to B can be seen clearly. All of the circular dots are “connected” to the square dots with R.There can be both finite and infinite ordered pairs. If a relation is taken from set A to itself, i.e. set A, it is generally characterized as ‘relation on A’. If set A (having p number of elements) has a relation with set B(having q number of elements) then the maximum number of relations is calculated as 2pq.
Domain and Range of a Relation:
Now, it’s crystal clear that a relation exactly like a Cartesian product has ordered pairs. In these ordered pairs, the second element is known to be the image of the first element, and the first element is known to be the preimage of the second element.
That means that among the two sets, one will have all the preimages and the other will have all the images. The domain of the relation is the set of all first elements of ordered pairs of relation.
Sometimes the domain set is different from set A as it can be seen in fig.1. While the set which contains the second element of all ordered pair is the range of the relation Now, here is a catch. The set B(the second one) can be equal to the range of the relation or it can be bigger than that. This happens in the case when elements in B are not related to any element of set A. That’s the reason why the whole set B is known by a different term i.e.
the codomain of the relation. It is crystal clear that
Range ⊆ Codomain
Relations are also represented in the way in which we represent sets, i.e. Roster method or Set-builder method. Another better representation is given by the arrow diagrams (Fig. 1).
For example, let there be a set N = {9,10,11,12,13}. Now, let there be a relation A from N to N similar in the ordered pair (x,y) in A, y is two more than x. There are three following different ways to show this:
- Set-builder method, here A = { (x,y):y = x + 2,x , y ∈ N}
- Roster method. Here A = { (9,11) , (10,12), (11,13)}
- You can see the arrow diagram:
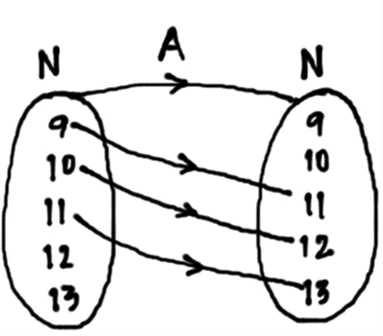
In this case, the domain of relation A is not N. It is equal to {9,10,11}. This is because of the other values from N, the output doesn’t fall in set N. Codomain of A also N, but the range of A is {11,12,13}, which is a subset of the codomain
Related Videos:
- Definition and arrow diagram of Function
- Explain Constant function with graph
- Description of function
- Explain Equal function with some example
- Explain Real valued function with some examples
- Domain codomain and range of function
Solved Examples
Example 1: What is the range of a Signum function.
Solution:
The real function f: F → F specified by
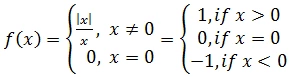
Example 2: Express the function f: X—R.f(y) = y2 – 1. where X = { -3, 0, 1, 3) as a set of ordered pairs.
Solution:
Given,
X = {-3, 0, 1, 3}
f(y) = y2 – 1
f(-3) = (-3)2 – 1 = 9 – 1=8
f(0) = (0)2 – 1 = -1
f(1) = (1)2 – 1 = 0
f(3) = (3)2 – 1 = 9 – 1 =8
Hence, the set of ordered pairs = {(-3, 8), (0, -1), (1, 0), (3, 8)}
Example 3: Let f(y) = y2 and g(y) = 2y + 1 are real functions. Find (f + g) (y), (f –g) (y), (fg) (y), (f/g ) (y)
Solution:
Given,
f(y) = y2 and g(y) = 2y + 1
(f + g) (y) = y2 + 2y + 1
(f – g) (y) = y2 -(2y + 1) = y2 – 2y – 1
(fg) (y) = y2(2y + 1) = 2y3 + y2
(f/g) (y) = y2/(2y + 1), y ≠ -1/2
Example 4: Assume that P = {1, 2, 3,…,14}. Express a relation F from P to P by F = {(a, b) : 3a – b = 0, such that a, b ∈ P}. Find and write down its range, domain, and codomain.
Solution:
It has been given that the relation F from P to P is specified by F = {(a, b): 3a – b = 0, where a, b ∈ P}.
Which means that F = {(a,b) : 3a = b, where a, b ∈ P}
Hence, F = {(1, 3), (2, 6), (3, 9), (4, 12)}
Set of all first elements of the ordered pairs in given relation is known to be the domain.
Hence, the domain of F is {1, 2, 3, 4}
To find the codomain, we know that the entire set A is the codomain of the relation F.
Hence, the codomain of F = A is {1, 2, 3,…,14}
As it is known that, the range of F is defined as the set of all second elements of the relation ordered pair.
Hence, the Range of F is {3, 6, 9, 12}
Important Chapters:


Similar Questions
Knowledge Check
What is a function of a keyboard in computer ?
APrintBInputCTypeDIn between input and outputWhat is the function of stomata?
ATrapping solar energy.BExchange of gases like carbon dioxide and oxygen.CPreparation of food.DBoth (b) and ( c)
