What is the smallest natural number n such that n! is divisible by 990
A
9
B
11
C
33
D
99
Video Solution
Text Solution
The correct Answer is:B
Consider option 'a'
Let us take n = 9
Since, 9!=9×8×7×6×5×4×3×2×1=362880
Which is not divisible by 990.
Now assume, n = 11
Since 11!=39916800
which is divisible by 990
thus, required smallest natural number 11
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
What is the sum of first n natural numbers ?
An(n−1)2Bn2(n−2)Cn(n+1)2Dn(n+2)2What is the mean of n odd natural numbers.
(a)n
(b)n+12
(c)n(n+1)2
(d)n+1AnBn+12Cn(n+1)2Dn+1if n is the smallest natural number such that n+2n+3n+⋅⋅⋅⋅⋅⋅⋅+99n is a perfect squre , then the number of digits in n2 is -
A1B2C3Dmore than 3
If N=23×37, then
What is the smallest number that you need to divisible by N in order to make it a perfect square ?
View SolutionTotal number of two digit number n What is the value of n such that (3n+7n) is divisible by 10
View SolutionIf n is the smallest natural number such that n+2n+3n+...+99n is a perfect square, then the number of digits in n2 is
View SolutionComplete the following statements.
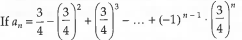 and bn=1−an then the smallest natural number n0, such that bn>anVntn>n0 is
and bn=1−an then the smallest natural number n0, such that bn>anVntn>n0 is
View SolutionFor every natural number n, n(n2−1) is divisible by
View Solution
