Question

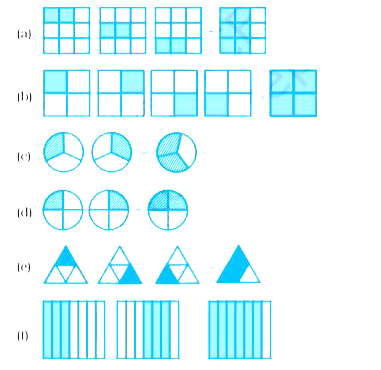
Which of the drawings (a) to (d) show : (i) $2\times \frac{1}{5}$ (ii) $2\times \frac{1}{2}$ (iii) $3\times \frac{2}{3}$ (iv) $3\times \frac{1}{4}$

Explanation

To solve the question, we need to identify which drawings (a) to (d) correspond to the given fractions and mixed numbers. Let's break down each part step by step.

Step 1: Identify `2 x 1/5`
1. Understanding `1/5`: This means one whole is divided into 5 equal parts.
2. Finding `2 x 1/5`: This means we need two of those parts. So, we are looking for a drawing that shows 5 equal sections, and we need to highlight 2 of those sections.
3. Check the drawings:
- Drawing A: Divided into 3 parts (not suitable).
- Drawing B: Divided into 4 parts (not suitable).
- Drawing C: Divided into 5 parts (correct).
- Drawing D: Divided into 5 parts (correct).
4. Conclusion: The correct drawing for `2 x 1/5` is Drawing D.

Step 2: Identify `2 x 1/2`
1. Understanding `1/2`: This means one whole is divided into 2 equal parts.
2. Finding `2 x 1/2`: This means we need two of those halves, which is equivalent to one whole.
3. Check the drawings:
- Drawing A: Shows 2 parts (not suitable).
- Drawing B: Shows 2 halves (correct).
- Drawing C: Shows 4 parts (not suitable).
- Drawing D: Shows 5 parts (not suitable).
4. Conclusion: The correct drawing for `2 x 1/2` is Drawing B.

Step 3: Identify `3 x 2/3`
1. Understanding `2/3`: This means one whole is divided into 3 equal parts, and we are considering 2 of those parts.
2. Finding `3 x 2/3`: This means we need three times the `2/3`, which can be visualized as having three groups of 2 parts out of 3.
3. Check the drawings:
- Drawing A: Shows 3 parts, and if we take 2 parts from each, it matches (correct).
- Drawing B: Shows 2 parts (not suitable).
- Drawing C: Shows 4 parts (not suitable).
- Drawing D: Shows 5 parts (not suitable).
4. Conclusion: The correct drawing for `3 x 2/3` is Drawing A.

Step 4: Identify `3 x 1/4`
1. Understanding `1/4`: This means one whole is divided into 4 equal parts.
2. Finding `3 x 1/4`: This means we need three of those quarters.
3. Check the drawings:
- Drawing A: Shows 3 parts (not suitable).
- Drawing B: Shows 2 parts (not suitable).
- Drawing C: Shows 4 parts (correct).
- Drawing D: Shows 5 parts (not suitable).
4. Conclusion: The correct drawing for `3 x 1/4` is Drawing C.

Final Answers:
- (i) `2 x 1/5` - Drawing D
- (ii) `2 x 1/2` - Drawing B
- (iii) `3 x 2/3` - Drawing A
- (iv) `3 x 1/4` - Drawing C