Which of the following cannot be valid assignment of probability for elementary events or outcomes of samples space S={w1,w2,w3,w4,w5,w6,w7}: Elementary events w1 w2 w3 w4 w5 w6 w7 i. 0.1 0.01 0.05 0.03 0.01 0.2 0.6 ii. 17 17 17 17 17 17 17 iii. 0.7 0.6 0.5 0.4 0.3 0.2 0.1 iv. 114 214 314 414 514 614 1514
Step by step video & image solution for Which of the following cannot be valid assignment of probability for elementary events or outcomes of samples space S={w_1, w_2, w_3, w_4, w_5, w_6, w_7}: Elementary events w_1 w_2 w_3 w_4 w_5 w_6 w_7 i. 0.1 0.01 0.05 0.03 0.01 0.2 0.6 ii. 1/7 1/7 1/7 1/7 1/7 1/7 1/7 iii. 0.7 0.6 0.5 0.4 0.3 0.2 0.1 iv. 1/(14) 2/(14) 3/(14) 4/(14) 5/(14) 6/(14) (15)/(14) by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROBABILITYBOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - MISCELLANEOUS EXERCISE ON CHAPTER
11 Videos
- PROBABILITYBOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - QUESTIONS FROM NCERT EXEMPLAR
5 Videos
- PROBABILITYBOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - NCERT-FILE (EXERCISE 16.2 )
6 Videos
- PERMUTATIONS AND COMBINATIONS BOOK - MODERN PUBLICATIONCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - CHAPTER TEST
12 Videos
- RELATIONS AND FUNCTIONSBOOK - MODERN PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Chapter Test
11 Videos
Similar Questions
Which of the following cannot be valid assignment of probabilities for outcomes of sample space S={W1,W2,W3,W4,W5,W6,W7}
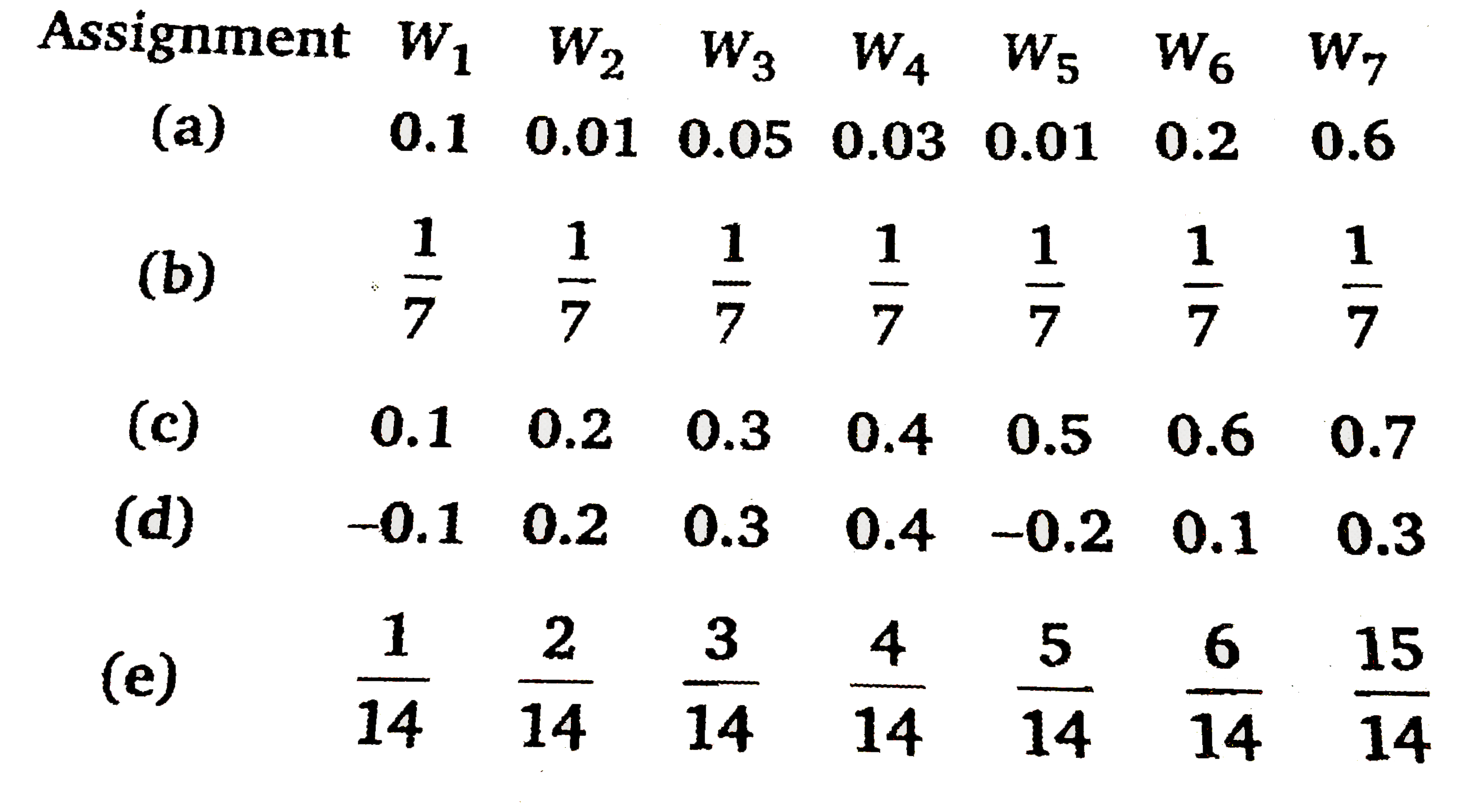
View SolutionWhich of the following can be the valid assignment of probability for outcomes of sample space, S={W1,W2,W3},{ where W1,W2 and W3 are mutually exclusive events
Assignment
w1w2w3(a)0.40.20.8(b)001(c)−123412(d)121214
View Solution
Knowledge Check
If ω is an imaginary cube root of unity, then (1−ω−ω2)7 equals
A128ωB−128ωC128ω2D−128ω2
Which of the following cannot be valid assignmentof probabilities for outcomes of sample space
S={ω1,ω2,ω3,ω4,ω5,ω6,ω7}?
Assignement ω1,ω2,ω3,ω4,ω5,ω6,ω7
a. 0.1,0.01,0.05,0.03,0.01,0.3,0.6
b. 17,17,17,17,17,17,17
c. 0.1,0.2,0.3,0.4,0.5,0.6,0.7
d. -0.1,0.2,0.3,0.4,-0.2,0.1,0.3
e. 114,214,314,414,514,614,1514
View SolutionIf ω be an imaginary cube root of unity, show that 1+ωn+ω2n=0, for n=2,4.
View Solution11+2ω+12+ω−11+ω=0
View SolutionIf w be an imaginary cube root of unity, show that 1+wn+w2n=0, for n=2,4.
View SolutionIf the complex number zandω satisfies z3+ω−7=0andz5⋅ω11=1 then
View SolutionIf the cube roots of unity are 1,ω,ω2, then the roots of the equation (x−1)3+8=0 are : (a) −1,1+2w,1+2w2 (b) −1,1−2w,1−2w2 (c) −1,−1,−1 (d) 1,w,w2
View SolutionUsing elementary transformations, find the inverse of the following matrix ⎡⎢⎣2−144023−27⎤⎥⎦
View Solution
