Which of the following can be the valid assignment of probability for outcomes of sample space, S={W1,W2,W3},{ where W1,W2 and W3 are mutually exclusive events
Assignment
w1w2w3(a)0.40.20.8(b)001(c)−123412(d)121214
(a) We have, P(W1)=0.4,P(W2)=0.2 and P(W3)=0.8
∴0≤P(Wi)≤1, for each Wi∈S
But, P(W1)+P(W2)+P(W3)=0.4+0.2+0.8=1.4>1
Hence, this assignment is not valid.
(b) P(W1)=0,P(W2)=0,P(W3)=1
Here, 0≤P(W(i))≤1, where Wi∈S and P(W1)+P(W2)+P(W3)=1
Hence this assignment is valid.
(c) Here, P(W1)<0
So, axiom 1 is not satisfied
Hence, this assignment is not valid.
(d) Again, P(W1)+P(W2)+P(W3)=12+12+14=54>0
Hence, this assignment is not valid.
Topper's Solved these Questions
- PROBABILITYBOOK - AAKASH INSTITUTECHAPTER - PROBABILITYEXERCISE - TRY YOURSELF
36 Videos
- PROBABILITYBOOK - AAKASH INSTITUTECHAPTER - PROBABILITYEXERCISE - ASSIGNMENT (SECTION - A Competition Level Questions)
114 Videos
- PRINCIPLE OF MATHEMATICAL BOOK - AAKASH INSTITUTECHAPTER - PRINCIPLE OF MATHEMATICAL EXERCISE - Section-D:(Assertion-Reason Type Questions)
12 Videos
- RELATIONS AND FUNCTIONS BOOK - AAKASH INSTITUTECHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Assignment (Section - J) Aakash Challengers Questions
8 Videos
Similar Questions
Which of the following cannot be valid assignment of probabilities for outcomes of sample space S={W1,W2,W3,W4,W5,W6,W7}
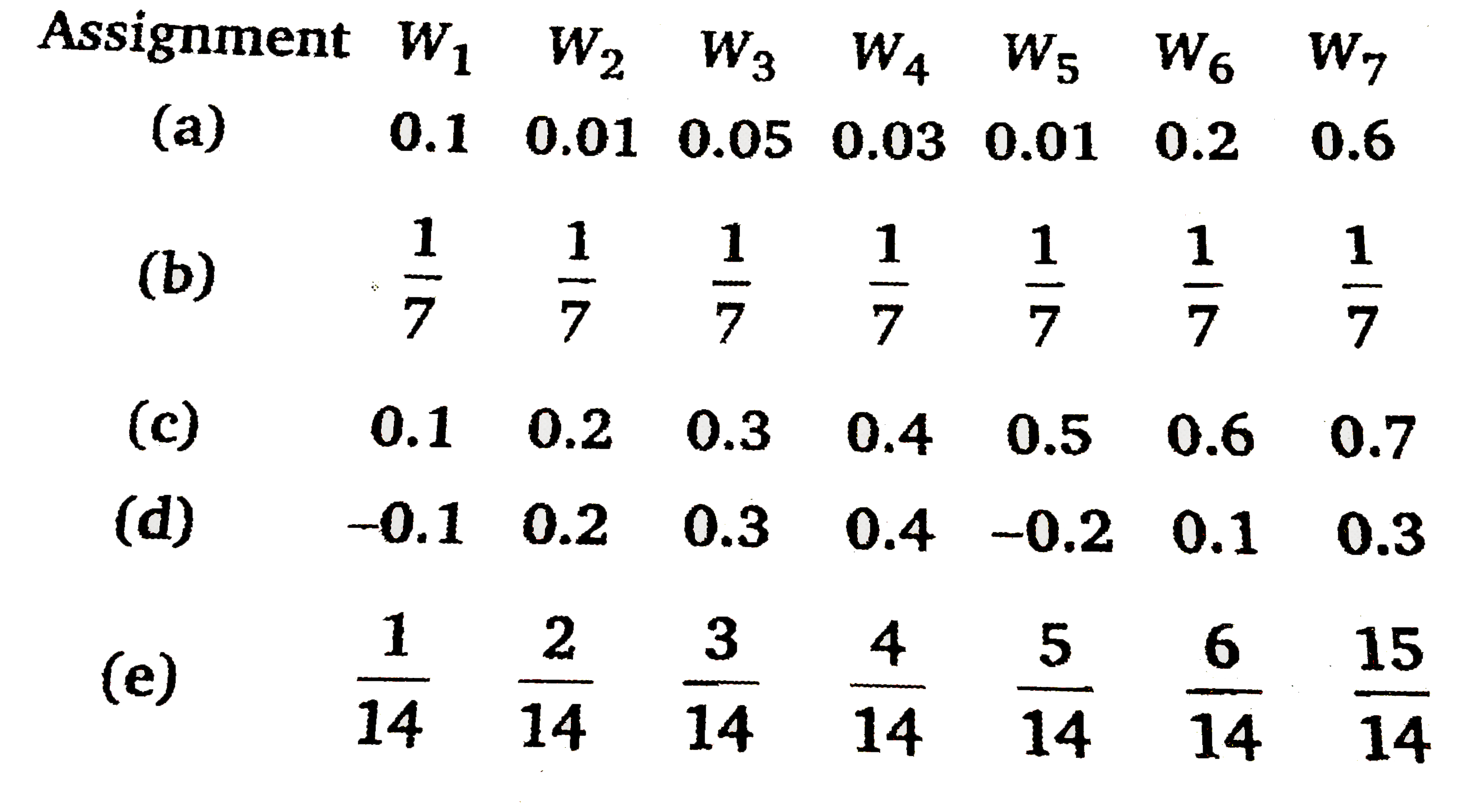
View SolutionWhich of the following cannot be valid assignment of probability for elementary events or outcomes of samples space S={w1,w2,w3,w4,w5,w6,w7}: Elementary events w1 w2 w3 w4 w5 w6 w7 i. 0.1 0.01 0.05 0.03 0.01 0.2 0.6 ii. 17 17 17 17 17 17 17 iii. 0.7 0.6 0.5 0.4 0.3 0.2 0.1 iv. 114 214 314 414 514 614 1514
View Solution
Knowledge Check
If W1:W2=2:3 and W1:W3=1:2 then W2:W3 is
A3:4B4:3C2:3D4:5If W1:W2=2:3 and W1:W3=1:2, then W2:W3 is:
A3:4B4:3C2:3D4:5In the circuit shown below E1=4.0V,R1=2Ω,E2=6.0V,R2=4Ω and R3=2Ω. The current I1 is
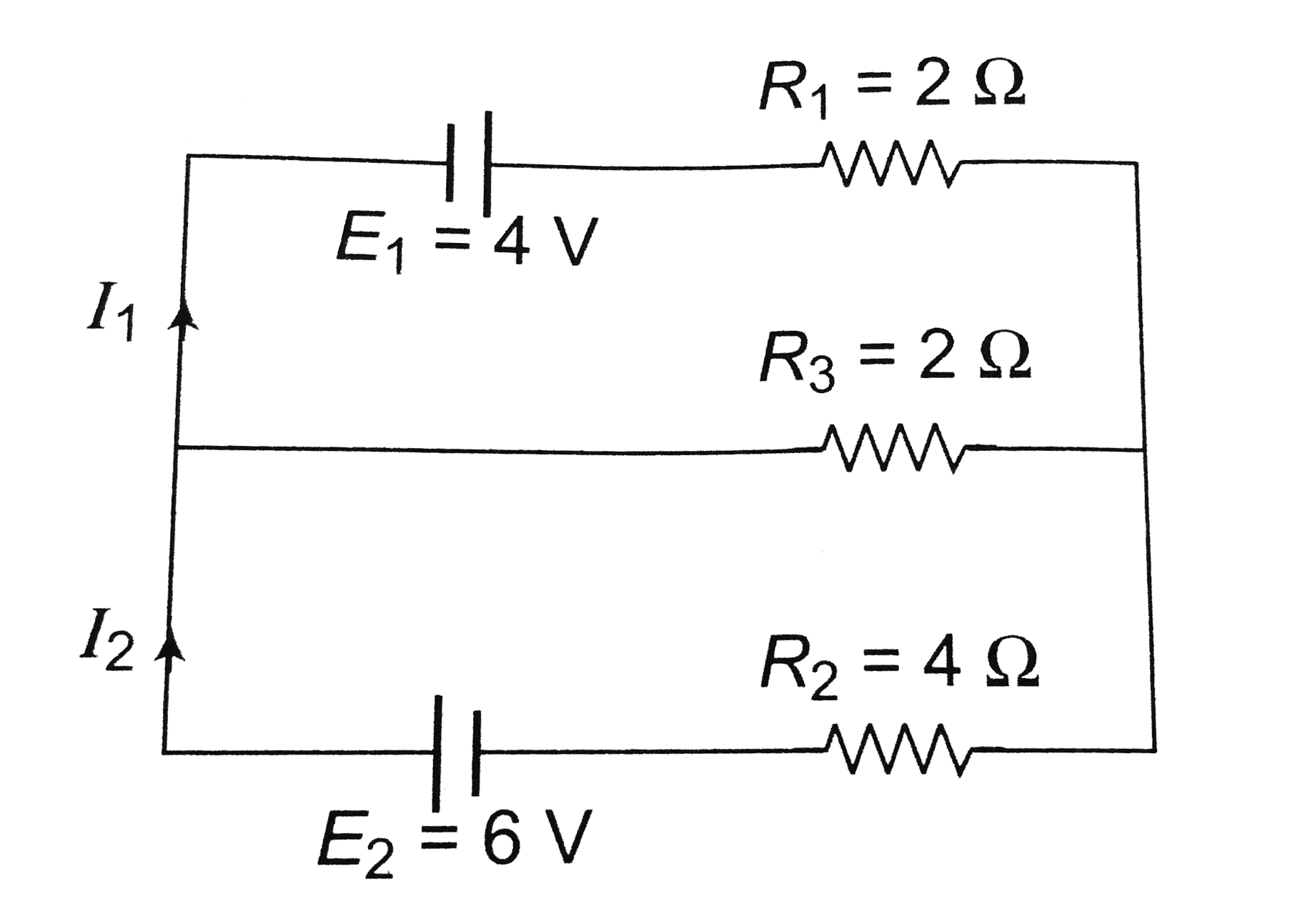 A1.6AB1.8AC1.25AD1.0A
A1.6AB1.8AC1.25AD1.0A
If 1,w,w2 are the cube roots of unity then 11+w2+21+w−3w2+w=
View SolutionWhich of the following is a non singular matrix? (A) ⎡⎢⎣1ab+c1bc+a1ca+b⎤⎥⎦ (B) ⎡⎢⎣1ωω2ωω21ω21ω⎤⎥⎦ where omega is non real and ω2=1 (C) ⎡⎢ ⎢⎣122232223242324252⎤⎥ ⎥⎦ (D) ⎡⎢⎣02−3−2053−50⎤⎥⎦
View Solution∣∣ ∣ ∣∣x+w2w1ww21+x1x+ww2∣∣ ∣ ∣∣=0
View SolutionLet z1=a+ib and z2=c+id are two complex number such that |z1|=|z2|=r and Re(z1z2)=0 . If w1=a+ic and w2=b+id, then (a)|w1|=r (b) |w2|=r (c)Re(w1w2)=0 (d) Im(w1w2)=0
View Solution1,ω,ω2 are the cube roots of unity, then the value of (1+ω)3−(1+ω2)3 is
View Solution
