Which of the following functions is neither odd nor even?
{(1,2),(4,7),(-1,2),(0,4),(-4,7)}
{(1,2),(4,7),(-1,-2),(0,0),(-4,-7)}
y=x3−1
y=x2−1
The correct Answer is:C
To determine which of the given functions is neither odd nor even, we need to analyze each option based on the definitions of odd and even functions.
Definitions:
1. Even Function: A function f(x) is called even if for every x in the domain, f(−x)=f(x).
2. Odd Function: A function f(x) is called odd if for every x in the domain, f(−x)=−f(x).
1. Check Option A:
- Let's denote the function as f(x).
- For x=1, suppose f(1)=2.
- For x=−1, suppose f(−1)=2.
- Since f(−1)=f(1), this means f(x) is even.
Conclusion for Option A: This function is even.
2. Check Option B:
- Let's denote the function as g(x).
- For x=1, suppose g(1)=2.
- For x=−1, suppose g(−1)=−2.
- Here, g(−1)=−g(1), which means g(x) is odd.
Conclusion for Option B: This function is odd.
3. Check Option C:
- Let's denote the function as h(x).
- For x=1, h(1)=13−1=0.
- For x=−1, h(−1)=(−1)3−1=−1−1=−2.
- Now, we check:
- For even: h(−1)≠h(1) (since −2≠0).
- For odd: h(−1)≠−h(1) (since −2≠−0).
- Therefore, this function does not satisfy the conditions for being either even or odd.
Conclusion for Option C: This function is neither odd nor even.
Final Answer:
The function that is neither odd nor even is Option C.
1. Even Function: A function f(x) is called even if for every x in the domain, f(−x)=f(x).
2. Odd Function: A function f(x) is called odd if for every x in the domain, f(−x)=−f(x).
- Let's denote the function as f(x).
- For x=1, suppose f(1)=2.
- For x=−1, suppose f(−1)=2.
- Since f(−1)=f(1), this means f(x) is even.
- Let's denote the function as g(x).
- For x=1, suppose g(1)=2.
- For x=−1, suppose g(−1)=−2.
- Here, g(−1)=−g(1), which means g(x) is odd.
- Let's denote the function as h(x).
- For x=1, h(1)=13−1=0.
- For x=−1, h(−1)=(−1)3−1=−1−1=−2.
- Now, we check:
- For even: h(−1)≠h(1) (since −2≠0).
- For odd: h(−1)≠−h(1) (since −2≠−0).
- Therefore, this function does not satisfy the conditions for being either even or odd.
The function that is neither odd nor even is Option C.
Topper's Solved these Questions
Similar Questions
If {(3,2),(4,2),(3,1),(7,1),(2,3)} is to be a function, which one of the following must be removed from the set?
01:39View SolutionIf xa⋅(xa+1)a⋅(xa)1−a=xk, then k=
01:38View Solution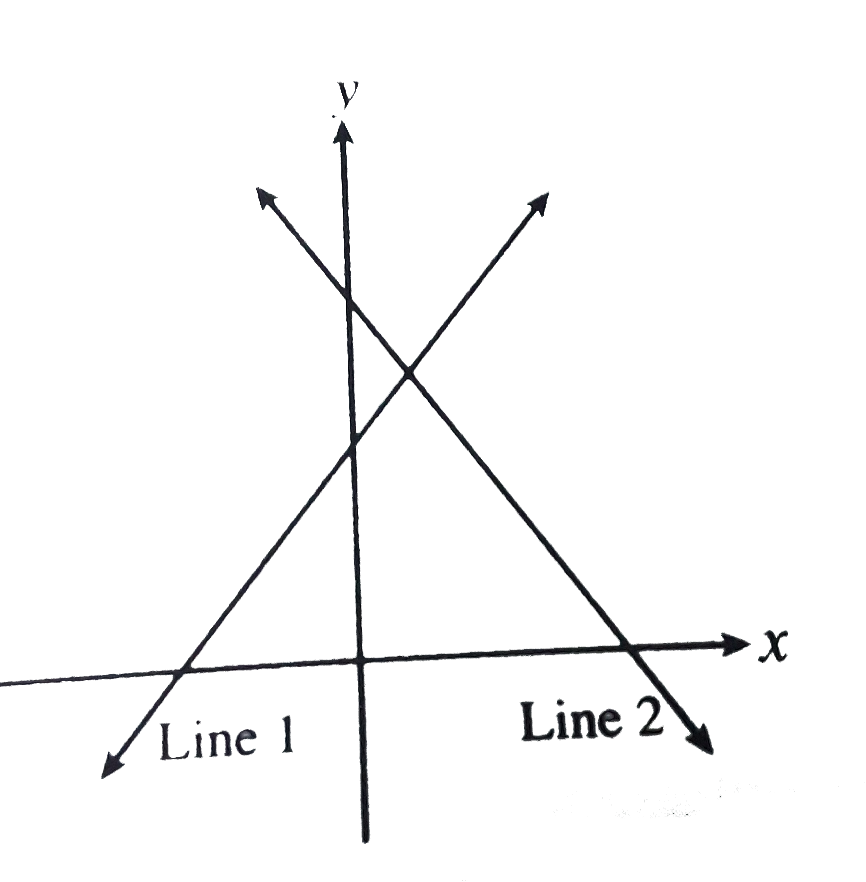
Consider two lines in the xy-plane , as shown above. If line 1 has equation y=m1x+b1, and line 2 has equation y=m2x+b2. Which is a true statement ?01:25View SolutionCategorize the following functions as odd/even/neither odd nor even functions. Justify your answer : (a)f(x)=x^(3)
01:35View SolutionDetermine whether the following functions are even or odd or neither even nor odd:
sin(x2+1)01:22View SolutionDetermine whether the following functions are even or odd or neither even nor odd:
x+x202:20View SolutionDetermine whether the following functions are even or odd or neither even nor odd:
f(x)=sinx+cosx03:36View SolutionDetermine whether the following functions are even or odd or neither even nor odd:
f(x)=(x2−1)|x|05:44View SolutionDetermine whether the following function are even/odd/neither even nor odd?
f(x)=ex+e−xex−e−x01:09View SolutionDetermine whether the following function are even/odd/neither even nor odd?
f:[−2,3]→[0,9],f(x)=x207:19View Solutionनिम्नलिखित फलनों में से कौन-सा एक न तो सम है, न ही विषम?
01:26View Solutionlog(x−3) is
(A) is an even function (B) an odd function (C) neither even nor odd (D) cannot be determined01:43View SolutionWhich of the following functions is (are) even, odd or neither:
03:05View SolutionDetermine whether the following functions are even or odd or neither even nor odd:
sin(x2+1)01:52View SolutionDetermine whether the following functions are even or odd or neither even nor odd:
x+x201:28View Solution

