Which of the following graph has more than three distinct real roots?
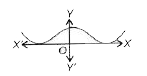



The correct Answer is:C
To determine which of the given graphs has more than three distinct real roots, we can follow these steps:
1. Understand the Concept of Roots:
- Roots of a polynomial are the values of x where the polynomial equals zero. Graphically, these are the points where the graph intersects the x-axis.
2. Identify the Criteria:
- We are looking for a graph that intersects the x-axis more than three times. This means we need to find a graph that has at least four points of intersection with the x-axis.
3. Analyze Each Graph:
- Graph A: Check how many times it intersects the x-axis. If it intersects twice, it has two distinct real roots.
- Graph B: Check how many times it intersects the x-axis. If it intersects three times, it has three distinct real roots.
- Graph C: Check how many times it intersects the x-axis. If it intersects four times, it has four distinct real roots.
- Graph D: Check how many times it intersects the x-axis. If it intersects only once, it has one real root.
4. Conclusion:
- After analyzing the graphs, we find that only Graph C intersects the x-axis four times. Therefore, it has more than three distinct real roots.
Final Answer:
- The graph that has more than three distinct real roots is Graph C.
- Roots of a polynomial are the values of x where the polynomial equals zero. Graphically, these are the points where the graph intersects the x-axis.
- We are looking for a graph that intersects the x-axis more than three times. This means we need to find a graph that has at least four points of intersection with the x-axis.
- Graph A: Check how many times it intersects the x-axis. If it intersects twice, it has two distinct real roots.
- Graph B: Check how many times it intersects the x-axis. If it intersects three times, it has three distinct real roots.
- Graph C: Check how many times it intersects the x-axis. If it intersects four times, it has four distinct real roots.
- Graph D: Check how many times it intersects the x-axis. If it intersects only once, it has one real root.
- After analyzing the graphs, we find that only Graph C intersects the x-axis four times. Therefore, it has more than three distinct real roots.
- The graph that has more than three distinct real roots is Graph C.
Topper's Solved these Questions
- POLYNOMIALS BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - POLYNOMIALS EXERCISE - EVERYDAY MATHEMATICS
6 Videos
- POLYNOMIALS BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - POLYNOMIALS EXERCISE - ACHIEVERS SECTION ( HOTS)
3 Videos
- PAIR OF LINEAR EQUATIONS IN TWO VARIABLESBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - PAIR OF LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Achievers Section (HOTS)
3 Videos
- PROBABILITYBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - PROBABILITYEXERCISE - ACHIEVERS SECTION (HOTS)
3 Videos
Similar Questions
Knowledge Check
Which of the following figures has more than three lines of symmetry?
A B
B C
C D
D
Which of the following have real root .
A2x2+x+1=0Bx2+x+1=0Cx2−6x+6=0D2x2+15x+30=0Which of the following equations has real and distinct roots ?
A3x2−6x+2=0B3x2−6x+3=0Cx2−8x+16=0D4x2−8x+4=0
Which of the following equations has real roots ?
View SolutionWhich of the following equations has real roots?
View SolutionWhich of the following equations has real roots ?
View SolutionWhich of the following has more electrons than neutrons?
View SolutionWhich of the following has more electrons than neutrons?
View Solution
