Which of the following is/are +ve ?
logsin1tan1
logcos1(1+tan3)
loglog105(cosθ+secθ)
logtan15∘(2sin18∘)
The correct Answer is:B, D
To determine which of the given options are positive, we will analyze each option using properties of logarithms and the values of trigonometric functions.
1. Option 1: log(tan(1)) to the base sin(1)
- We need to check the values of tan(1) and sin(1).
- tan(1 radian) is greater than 1.
- sin(1 radian) is less than 1.
- Since tan(1) > 1 and sin(1) < 1, they lie on opposite sides of 1.
- Therefore, log(tan(1)) to the base sin(1) is negative.
- Conclusion: This option is rejected.
2. Option 2: log(1 + tan(3)) to the base cos(1)
- We need to evaluate 1 + tan(3).
- tan(3 radians) is negative, hence 1 + tan(3) < 1.
- cos(1 radian) is also less than 1.
- Since both values (1 + tan(3) and cos(1)) are less than 1, they lie on the same side of 1.
- Therefore, log(1 + tan(3)) to the base cos(1) is positive.
- Conclusion: This option is accepted.
3. Option 3: log(cos(θ) + sec(θ)) to the base log(5) to the base 10
- We can express cos(θ) + sec(θ) as (cos²(θ) + 1) / cos(θ).
- The numerator (cos²(θ) + 1) is always greater than 1 (since cos²(θ) is between 0 and 1).
- The denominator (cos(θ)) is also between 0 and 1.
- Thus, cos(θ) + sec(θ) > 1.
- log(5) to the base 10 is less than 1.
- Since we have one value greater than 1 and the other less than 1, this logarithm will be negative.
- Conclusion: This option is rejected.
4. Option 4: log(sin(18)) to the base tan(15)
- We know that sin(18) is approximately (√5 - 1) / 4, which is slightly less than 1.
- tan(15) is also less than 1.
- Since both sin(18) and tan(15) are less than 1, they lie on the same side of 1.
- Therefore, log(sin(18)) to the base tan(15) is positive.
- Conclusion: This option is accepted.
Final Answer:
The options that are positive are Option 2 and Option 4.
- We need to check the values of tan(1) and sin(1).
- tan(1 radian) is greater than 1.
- sin(1 radian) is less than 1.
- Since tan(1) > 1 and sin(1) < 1, they lie on opposite sides of 1.
- Therefore, log(tan(1)) to the base sin(1) is negative.
- Conclusion: This option is rejected.
- We need to evaluate 1 + tan(3).
- tan(3 radians) is negative, hence 1 + tan(3) < 1.
- cos(1 radian) is also less than 1.
- Since both values (1 + tan(3) and cos(1)) are less than 1, they lie on the same side of 1.
- Therefore, log(1 + tan(3)) to the base cos(1) is positive.
- Conclusion: This option is accepted.
- We can express cos(θ) + sec(θ) as (cos²(θ) + 1) / cos(θ).
- The numerator (cos²(θ) + 1) is always greater than 1 (since cos²(θ) is between 0 and 1).
- The denominator (cos(θ)) is also between 0 and 1.
- Thus, cos(θ) + sec(θ) > 1.
- log(5) to the base 10 is less than 1.
- Since we have one value greater than 1 and the other less than 1, this logarithm will be negative.
- Conclusion: This option is rejected.
- We know that sin(18) is approximately (√5 - 1) / 4, which is slightly less than 1.
- tan(15) is also less than 1.
- Since both sin(18) and tan(15) are less than 1, they lie on the same side of 1.
- Therefore, log(sin(18)) to the base tan(15) is positive.
- Conclusion: This option is accepted.
The options that are positive are Option 2 and Option 4.
Topper's Solved these Questions
- COMPOUND ANGLESBook:VIKAS GUPTA (BLACK BOOK) ENGLISHChapter:COMPOUND ANGLESExercise:Exercise-3 : Comprehension Type Problems
Explore 12 Videos
- COMPOUND ANGLESBook:VIKAS GUPTA (BLACK BOOK) ENGLISHChapter:COMPOUND ANGLESExercise:Exercise-4 : Matching Type Problems
Explore 5 Videos
- COMPOUND ANGLESBook:VIKAS GUPTA (BLACK BOOK) ENGLISHChapter:COMPOUND ANGLESExercise:Exercise-5 : Subjective Type Problems
Explore 31 Videos
- COMPLEX NUMBERSBook:VIKAS GUPTA (BLACK BOOK) ENGLISHChapter:COMPLEX NUMBERSExercise:EXERCISE-5 : SUBJECTIVE TYPE PROBLEMS
Explore 8 Videos
- CONTINUITY, DIFFERENTIABILITY AND DIFFERENTIATIONBook:VIKAS GUPTA (BLACK BOOK) ENGLISHChapter:CONTINUITY, DIFFERENTIABILITY AND DIFFERENTIATIONExercise:EXERCISE (SUBJECTIVE TYPE PROBLEMS)
Explore 24 Videos
Similar Questions
Which of the following can ve used as an emergency contraceptive to avoid possible pregnancy ?
View SolutionWhich of the following is correct for electron gain enthalpy (with -ve sign) of halogens?
View SolutionAB(s)⇔A(g)+B(g)Kp=4,ΔH=+ve
In a container,A(g) "and" B(g) are filled to partial pressure of 1 atm each. Now AB(s) is added (in excess quantity). Which of the following is CORRECT? (No other gas is present in container):
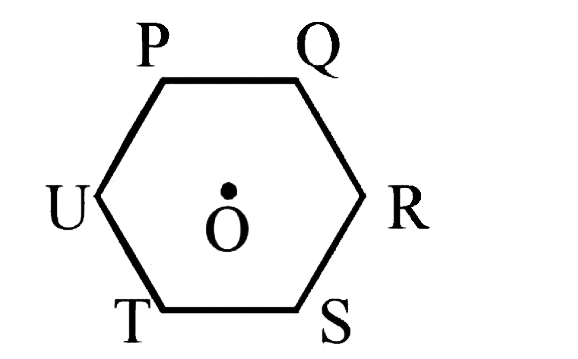
View Solutionsix charges of equal magnitude, 3 poistive and 3 negative are to be placed on PQRSTU corners of a regular hexagon, such that field at the centre is double that of what it would have been if only one +ve charge is placed at R. Which of the following arrangement of charge is posisble for P, Q, R, S, T and U respectively.
View SolutionFor the electron affinity of halogens (with −ve sign), which of the following is correct?
View SolutionAn unknown transistor needs to be identified as npn and pnp type. A multimeter, wilth +ve and −ve terminals is used to measure resistance between different terminals transistor. If terminal 2 is the base of the transistor then which of the following is correct for a pnp transistor?
View SolutionWhich one of the following is correctly matched :-
(i)z=1(A)−ve deviation(ii)z<1(B)+ve deviation(iii)z>1(C)Ideal behaviour(iv)zc=3/8(D)At crtical conditions
View SolutionA particle performs SHM along a straight line and its position is ¯¯¯R , acceleration is ¯a , velocity is ¯v is and force on particle is ¯f. Then which of the following statements are true?
ˆv⋅ˆa is always +ve
ˆv⋅ˆR may be -ve
ˆf⋅ˆR is always -ve
ˆv is parrallel to ¯f sometimes
View SolutionA particle performs SHM along a straight line and its position is →R, acceleration is →a, velocity is →v is and force on particle is →f. Then which of the following statement are true?
(i) →v.→a is always + ve
(ii) →v.→R may be -ve
(iii) →f.→R is always -ve
(iv) →v is parallel to →f sometimes
View SolutionWhich of the following conditions may lead to a non-spontaneous change?
a.ΔH and ΔS both +ve
b.ΔH=−ve,ΔS=+ve
c.ΔH=+ve,ΔS=−ve
d.ΔH=−ve,ΔS=−ve
View Solution