Which of the following is not an odd function ?
ln (x4+x2+1(x2+x+1)2)
sgn (sgn(x))
sin (tan x)
f(x), where f(x)+f(1x)=f(x)f(1x)∀x∈R−{0}andf(2)=33
The correct Answer is:D
To determine which of the given functions is not an odd function, we need to recall the definition of an odd function. A function f(x) is considered odd if it satisfies the condition:
f(−x)=−f(x)
Now, let's analyze each option step by step.
Step 1: Analyze Option 1
Function: f(x)=log(x4+x2+1)(x2+x+1)2
Check: We need to evaluate f(−x).
f(−x)=log((−x)4+(−x)2+1)((−x)2+(−x)+1)2
Calculating f(−x):
=log(x4+x2+1)(x2−x+1)2
Now, we compare f(−x) with −f(x):
−f(x)=−log(x4+x2+1)(x2+x+1)2
Since f(−x)≠−f(x), this function is not an odd function.
Step 2: Analyze Option 2
Function: f(x)=sin(sinx)
Check: Evaluate f(−x).
f(−x)=sin(sin(−x))=sin(−sinx)=−sin(sinx)=−f(x)
Since f(−x)=−f(x), this function is an odd function.
Step 3: Analyze Option 3
Function: f(x)=sin(tanx)
Check: Evaluate f(−x).
f(−x)=sin(tan(−x))=sin(−tanx)=−sin(tanx)=−f(x)
Since f(−x)=−f(x), this function is also an odd function.
Step 4: Analyze Option 4
Function: f(x) defined by the equation f(x)+f(1x)=f(x)⋅f(1x)
Check: We need to evaluate f(−x).
Substituting −x:
f(−x)+f(−1x)=f(−x)⋅f(−1x)
This does not directly help us show that f(−x)≠−f(x). However, we can analyze the implications of this equation.
Assuming f(x) is odd, we would have:
f(−x)+f(−1x)=−f(x)−f(1x)
This leads to contradictions based on the nature of f. Thus, we conclude that this function is not an odd function.
Conclusion
The functions that are not odd functions are:
1. Option 1: log(x4+x2+1)(x2+x+1)2
2. Option 4: f(x)+f(1x)=f(x)⋅f(1x)
Final Answer
The functions that are not odd functions are Option 1 and Option 4.
---
Function: f(x)=log(x4+x2+1)(x2+x+1)2
Function: f(x)=sin(sinx)
Function: f(x)=sin(tanx)
Function: f(x) defined by the equation f(x)+f(1x)=f(x)⋅f(1x)
The functions that are not odd functions are:
1. Option 1: log(x4+x2+1)(x2+x+1)2
2. Option 4: f(x)+f(1x)=f(x)⋅f(1x)
The functions that are not odd functions are Option 1 and Option 4.
Topper's Solved these Questions
- FUNCTION BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - FUNCTION EXERCISE - ONE OR MORE THAN ONE ANSWE IS/ARE CORRECT
23 Videos
- FUNCTION BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - FUNCTION EXERCISE - COMPREHENSION TYPE PROBLEMS
13 Videos
- ELLIPSE BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - ELLIPSE EXERCISE - Exercise-4 : Subjective Type Problems
2 Videos
- HYPERBOLABOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - HYPERBOLAEXERCISE - Exercise-4 : Subjective Type Problems
3 Videos
Similar Questions
Knowledge Check
Which of the following is an odd function?
I. f(x)=3x3+5
II. g(x)=4x6+2x4−3x2
III. h(x)=7x5−8x3+12xAonly IBonly IIConly IIIDonly I and IIIf f(x)=x3andg(x)=x2+1, which of the following is an odd functionn (are odd functions)?
I. f(x)⋅g(x)
II. f(g(x))
III. g(f(x))AOnly IBonly IIConly IIIDOnly II and IIIWhich of the following graphs is NOT a function ?
A B
B C
C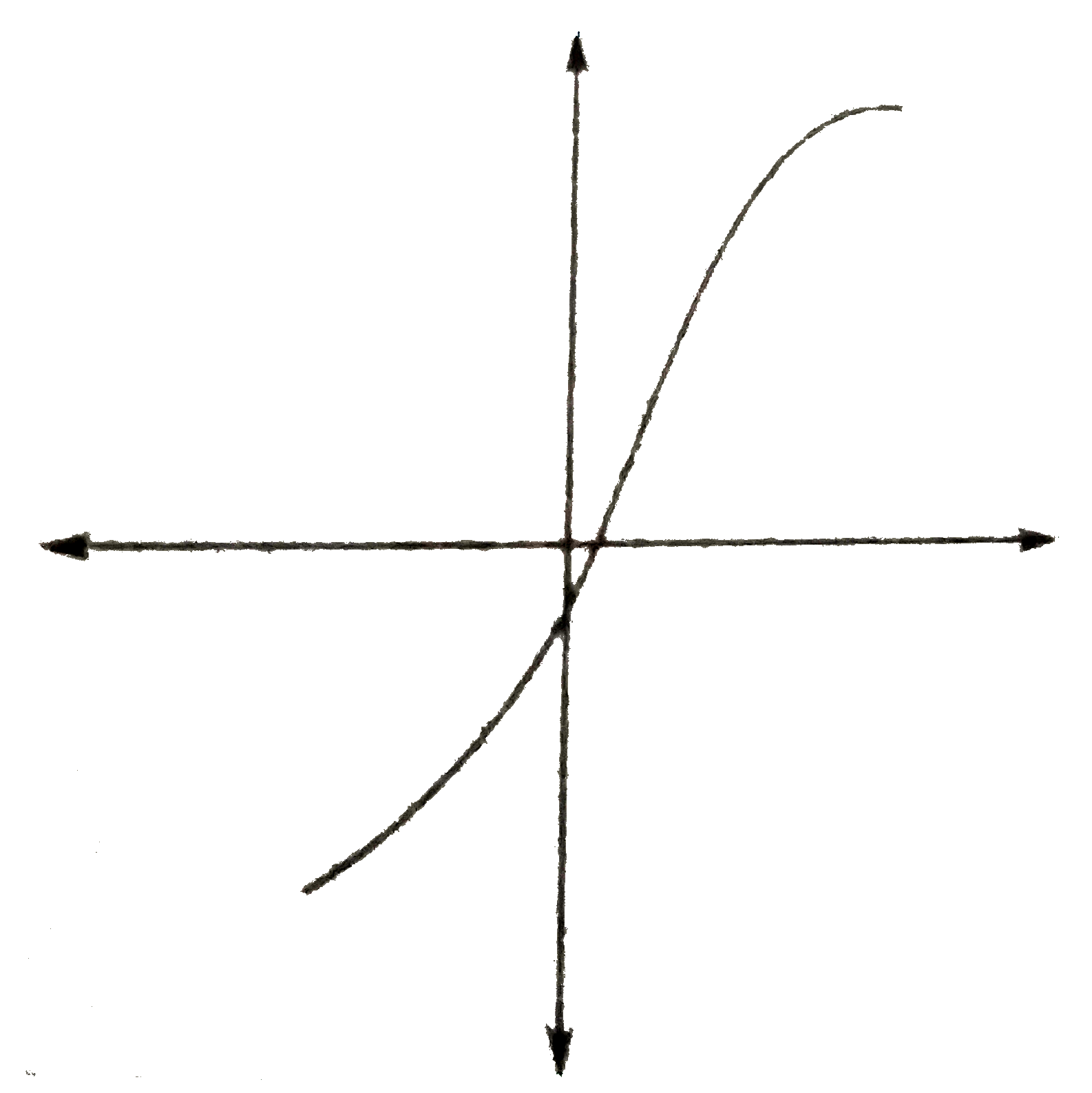 D
D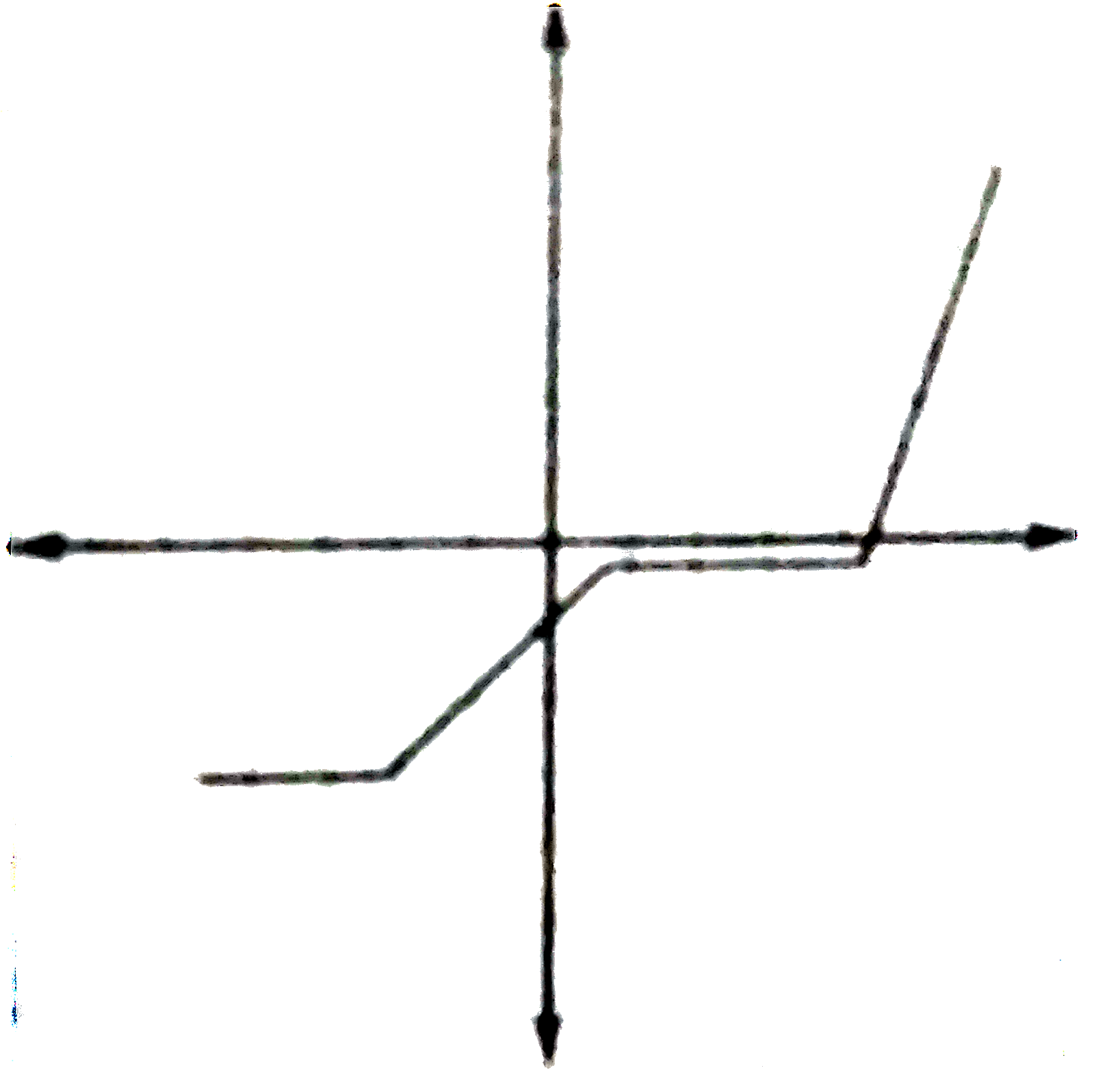
Which of the following functions is an odd function:
View SolutionWhich of the following is the odd one out ?
View SolutionWhich of the following is the odd one out ?
View SolutionWhich of the following is an odd electron molecule?
View SolutionWhich of the following relations is a function?
View Solution
