Which of the following is not the graph of a quadratic polynomial?

The correct Answer is:C:D
To determine which of the given options is not the graph of a quadratic polynomial, we can follow these steps:
1. Understand the Definition of a Quadratic Polynomial:
A quadratic polynomial is a polynomial of degree 2, which can be expressed in the standard form as ax2+bx+c, where a≠0. The graph of a quadratic polynomial is a parabola.
2. Identify the Characteristics of the Graph:
The key characteristic of the graph of a quadratic polynomial is that it can intersect the x-axis at most twice. This means:
- It can touch the x-axis at two points (two real roots).
- It can touch the x-axis at one point (one real root, also known as a double root).
- It can not touch the x-axis at all (no real roots).
3. Analyze the Given Options:
We need to analyze the graphs presented in the options:
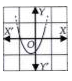
- Option 1: If the graph touches the x-axis at two points, it is a quadratic polynomial.
- Option 2: If the graph touches the x-axis at two points, it is also a quadratic polynomial.
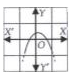
- Option 3: If the graph does not touch the x-axis at all (it lies completely above or below), it is not a quadratic polynomial.
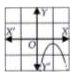
- Option 4: If the graph touches the x-axis at three points, it is also not a quadratic polynomial.
4. Conclusion:
Based on the analysis:
- Option 3 and Option 4 do not represent graphs of quadratic polynomials because:
- Option 3 does not intersect the x-axis (no real roots).
- Option 4 intersects the x-axis at three points (which is impossible for a quadratic polynomial).
Final Answer:
The options that are not graphs of a quadratic polynomial are Option 3 and Option 4.
---
A quadratic polynomial is a polynomial of degree 2, which can be expressed in the standard form as ax2+bx+c, where a≠0. The graph of a quadratic polynomial is a parabola.
The key characteristic of the graph of a quadratic polynomial is that it can intersect the x-axis at most twice. This means:
- It can touch the x-axis at two points (two real roots).
- It can touch the x-axis at one point (one real root, also known as a double root).
- It can not touch the x-axis at all (no real roots).
We need to analyze the graphs presented in the options:
- Option 1: If the graph touches the x-axis at two points, it is a quadratic polynomial.
- Option 2: If the graph touches the x-axis at two points, it is also a quadratic polynomial.
- Option 3: If the graph does not touch the x-axis at all (it lies completely above or below), it is not a quadratic polynomial.
- Option 4: If the graph touches the x-axis at three points, it is also not a quadratic polynomial.
Based on the analysis:
- Option 3 and Option 4 do not represent graphs of quadratic polynomials because:
- Option 3 does not intersect the x-axis (no real roots).
- Option 4 intersects the x-axis at three points (which is impossible for a quadratic polynomial).
The options that are not graphs of a quadratic polynomial are Option 3 and Option 4.
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - POLYNOMIALSEXERCISE - EXERCISE (Subjective Problems) (Integer/Numerical Value Type)10videos
POLYNOMIALS
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PAIR OF LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - NCERT SECTION (EXERCISE 3.7)18videos
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PROBABILITYEXERCISE - Olympiad/HOTS Corner26videos
PROBABILITY
Similar Questions
Knowledge Check
- Question 1 - Select One
Which of the following ig not a graph of a quadratic equation?
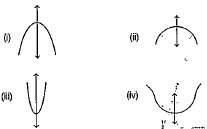 Aonly (iii)B(i) and (iii)C(ii) and (iv)Donly (iv)
Aonly (iii)B(i) and (iii)C(ii) and (iv)Donly (iv) - Question 2 - Select One or More
If a,b,c ∈R, then for which of the following graphs of the quadratic polynomial y=ax2−2bx+c(a≠0), the product (abc) is negative ?
A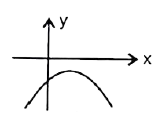 B
B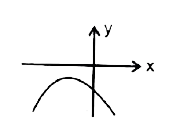 C
C D
D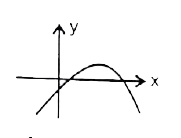
Graph of Quadratic Polynomial
View SolutionRange of Quadratic polynomial
View SolutionSign of a Quadratic Polynomial
View Solutionwhich one of the following can best represent the graph of quadratic polynomial y=ax2+bx+c (where a<0,b<0andc>0) ?
View SolutionRange of Quadratic Polynomial
View SolutionVertex of a Quadratic Polynomial
View Solution

