Question

Which of the following is the greates?
$\cos ec1$
(b) $\cos ec2$

$\cos ec4$
(d) $\cos ec(-6)$

Options

A. cosec 1
B. cosec 2
C. cosec 4
D. cosec (-6)

Answer

D

Explanation

(d) Consider sin , sin 2, and -sin6 (sin4 is negative , hence, cosec 4 cancot be maximum).
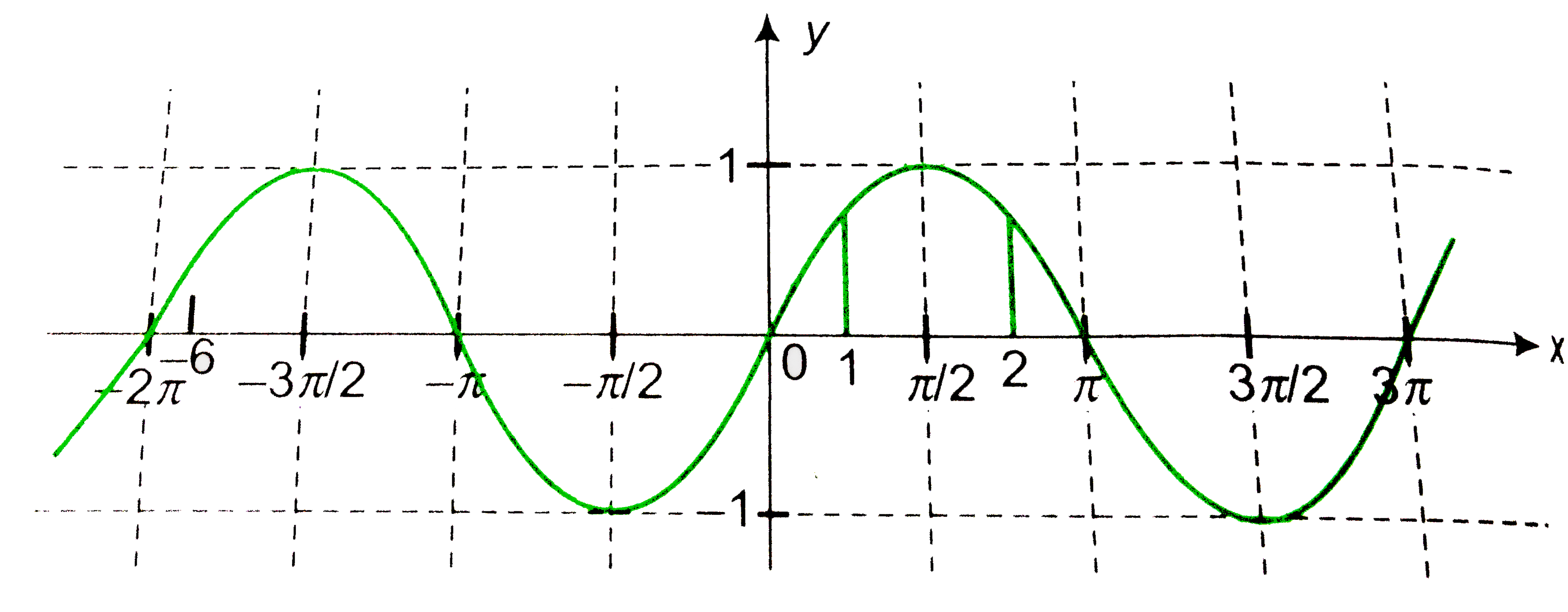From the graph, sin(-6) is least and positive hence, cosec(-6) is maximum.