Doubtnut Promotions Sticky

Which of the following options is INCORRECT?

A

The number of terms in the A.P, 3, 6, 9, 12,..., 111 is 37.

B

If the first three terms of an A.P. are x-1, x + 1 and 2x + 3, then the value of x is 0.

C

The sum of first 'n' natural numbers is [n(n+1)2]2

D

None of these

Video Solution
Doubtnut Promotions Banner
Text Solution
Generated By DoubtnutGPT

The correct Answer is:C

To solve the question of identifying the incorrect option, we will analyze each option step by step.

Step 1: Analyze Option 1
Statement: The number of terms in the AP (Arithmetic Progression) 3, 6, 9, ..., 111 is 37.

Solution:
1. Identify the first term a=3 and the last term l=111.
2. The common difference d=6−3=3.
3. Use the formula for the n-th term of an AP:
an=a+(n−1)⋅d
Setting an=111:
111=3+(n−1)⋅3
4. Rearranging gives:
111−3=(n−1)⋅3⟹108=(n−1)⋅3
5. Dividing both sides by 3:
n−1=36⟹n=37
Conclusion: Option 1 is correct.

Step 2: Analyze Option 2
Statement: The first three terms of an AP are x−1,x+1,2x+3. Then, the value of x is 0.

Solution:
1. For the terms to be in AP, the middle term must be the average of the other two:
x+1=(x−1)+(2x+3)2
2. Simplifying the right side:
x+1=x−1+2x+32=3x+22
3. Cross-multiply:
2(x+1)=3x+2⟹2x+2=3x+2
4. Rearranging gives:
2=3x−2x⟹x=0
Conclusion: Option 2 is correct.

Step 3: Analyze Option 3
Statement: The sum of the first n natural numbers is n(n+1)2=2.

Solution:
1. The formula for the sum of the first n natural numbers is indeed n(n+1)2.
2. Setting this equal to 2:
n(n+1)2=2
3. Multiplying both sides by 2:
n(n+1)=4
4. Rearranging gives:
n2+n−4=0
5. Using the quadratic formula n=−b±√b2−4ac2a:
n=−1±√1+162=−1±√172
6. Since n must be a natural number, there are no valid solutions for n in this case.
Conclusion: Option 3 is incorrect.

Final Answer
The incorrect option is Option 3.

|
Updated on:8/8/2024
Class 10MATHSIMO QUESTION PAPER 2018 SET A

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    ocr_image
    Which of the following combination is INCORRECT option ?

    A(i)(III)(R)
    B(III)(ii)(Q)
    C(III)(iv)(S)
    D(IV)(ii)(P)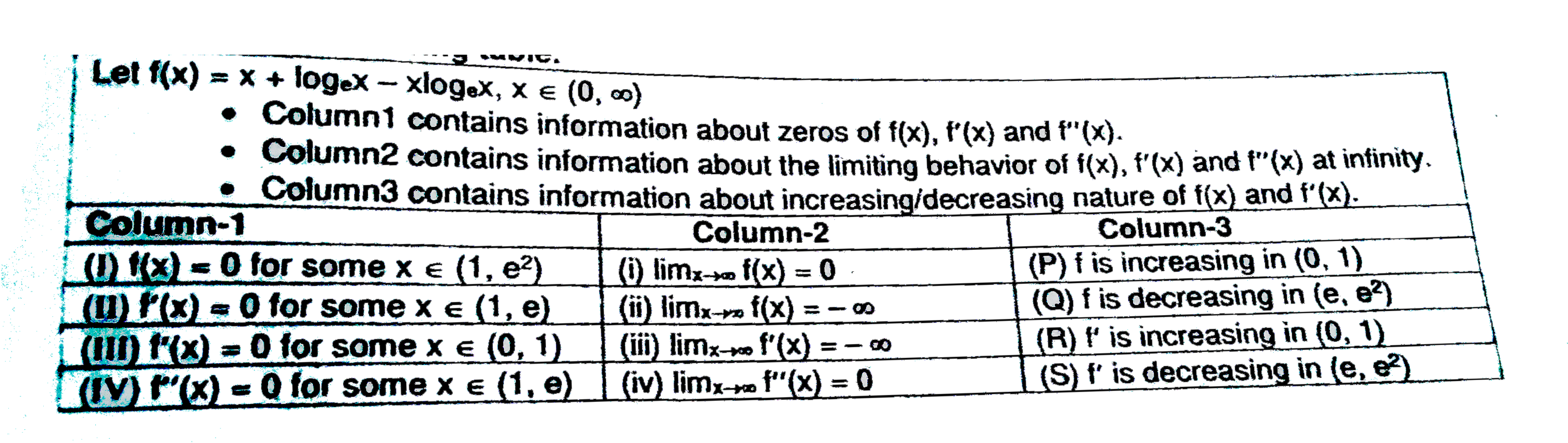
  • Question 2 - Select One

    ocr_image
    Which of the following options is the only INCORRECT combination ?

    A(I),(iii)(P)
    B(II)(iv)(Q)
    C(II),(iii)(P)
    D(III)(i)(R)
  • Question 3 - Select One

    ocr_image
    Which of the following options is the only INCORRECT combination ?

    A(III) (iii) (R)
    B(III) (iv) (S)
    C(IV) (i) (R)
    D(I) (ii) (Q)