Which of the following statements are correct? Write a correct form of each of the incorrect statements. (i) φ∈{a,b} (ii) φ⊂{a,b,c} (iii) {x:x+3=3}=φ
To determine the correctness of the given statements and to provide corrections for the incorrect ones, we will analyze each statement step by step.
1. Statement (i): φ∈{a,b}
- Here, φ (φ) represents the empty set. The statement claims that the empty set is an element of the set {a,b}.
- The set {a,b} contains the elements a and b, but it does not contain the empty set as an element.
- Therefore, this statement is incorrect.
Correct Form:
- The correct statement would be:
- φis¬∈{a,b} or
- {φ}∈{a,b} (if we want to say that the set containing the empty set is an element of a larger set).
2. Statement (ii): φ⊂{a,b,c}
- This statement claims that the empty set is a subset of the set {a,b,c}.
- By definition, the empty set is a subset of every set, including {a,b,c}.
- Therefore, this statement is correct.
3. Statement (iii): {x:x+3=3}=φ
- This statement describes a set of elements x such that x+3=3.
- Solving for x, we find that x=0. Thus, the set can be expressed as {0}.
- The statement claims that this set is equal to the empty set (φ), which is incorrect since {0} is not empty.
- Therefore, this statement is incorrect.
Correct Form:
- The correct statement would be:
- {x:x+3=3}={0}.
Summary of Statements:
- (i) Incorrect: φis¬∈{a,b} or {φ}∈{a,b}.
- (ii) Correct: φ⊂{a,b,c}.
- (iii) Incorrect: {x:x+3=3}={0}.
- Here, φ (φ) represents the empty set. The statement claims that the empty set is an element of the set {a,b}.
- The set {a,b} contains the elements a and b, but it does not contain the empty set as an element.
- Therefore, this statement is incorrect.
- The correct statement would be:
- φis¬∈{a,b} or
- {φ}∈{a,b} (if we want to say that the set containing the empty set is an element of a larger set).
- This statement claims that the empty set is a subset of the set {a,b,c}.
- By definition, the empty set is a subset of every set, including {a,b,c}.
- Therefore, this statement is correct.
- This statement describes a set of elements x such that x+3=3.
- Solving for x, we find that x=0. Thus, the set can be expressed as {0}.
- The statement claims that this set is equal to the empty set (φ), which is incorrect since {0} is not empty.
- Therefore, this statement is incorrect.
- The correct statement would be:
- {x:x+3=3}={0}.
- (i) Incorrect: φis¬∈{a,b} or {φ}∈{a,b}.
- (ii) Correct: φ⊂{a,b,c}.
- (iii) Incorrect: {x:x+3=3}={0}.
Topper's Solved these Questions
Similar Questions
Which of the following statements are correct? Write a correct form of each of the incorrect statements. (i) a⊂{a,b,c} (ii) {a}∈{a,b,c} (iii) a∈{{a},b}
View SolutionWhich of the following statements are correct? Write a correct form of each of the incorrect statements. (i) {a}⊂{{a},b} (ii) {b,c}⊂{a,{b,c}} (iii) {a,b}⊂{b,c}
View SolutionWhich of the following statement is/are correct regarding B-F bond in BF3?
View SolutionWhich of the following statements regarding the compound AxBy is /are correct?
View SolutionWhich of the following statements are correct for van't Hoff factor 'i' for a solution of weak electrolyte AxBy?
View SolutionGiven a+b+c+d=0. Which of the following statements(s) is (are) correct?
View Solution
Which statements are correct for reagents A, B, C, and D?View Solution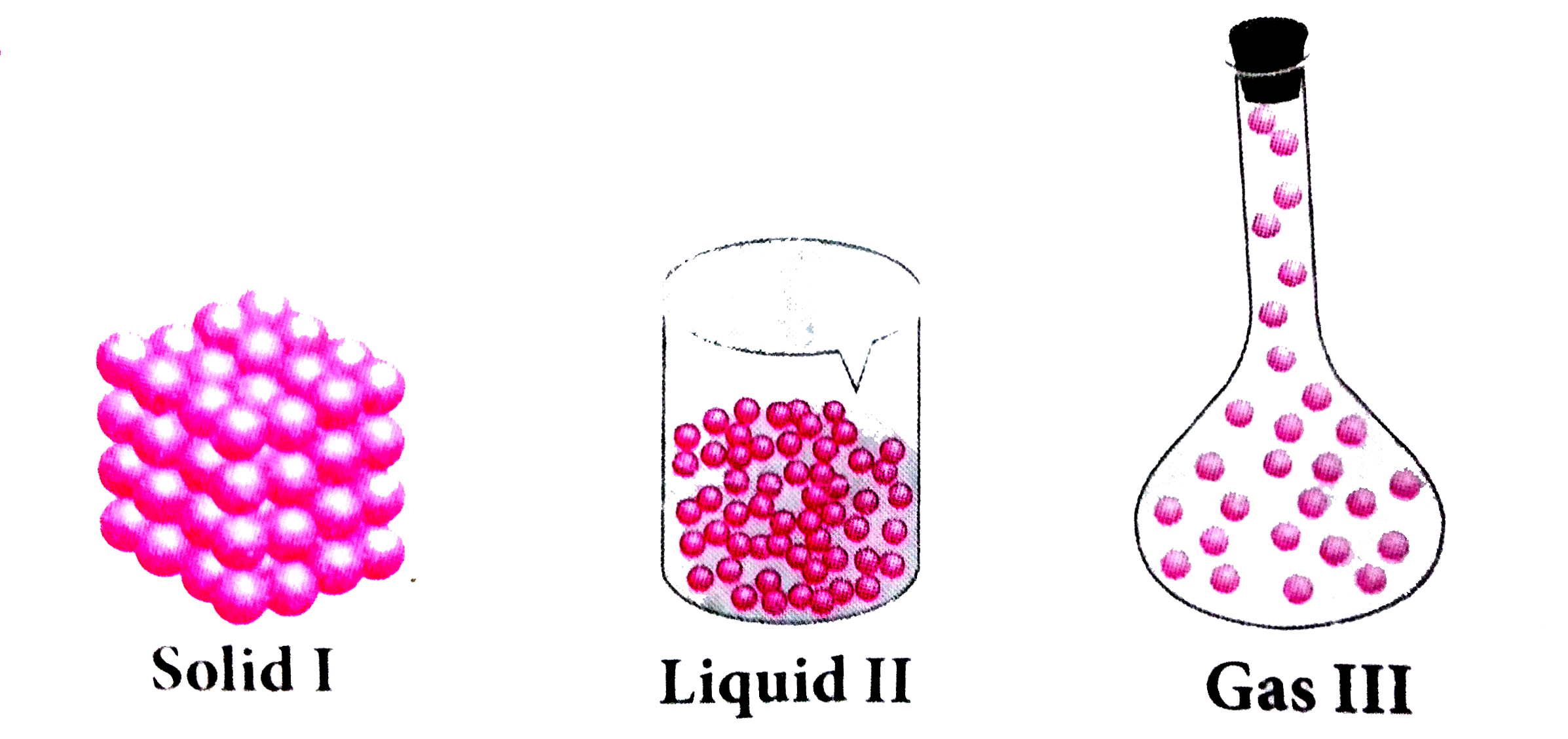
Choose the correct statement about I, II and III.View Solution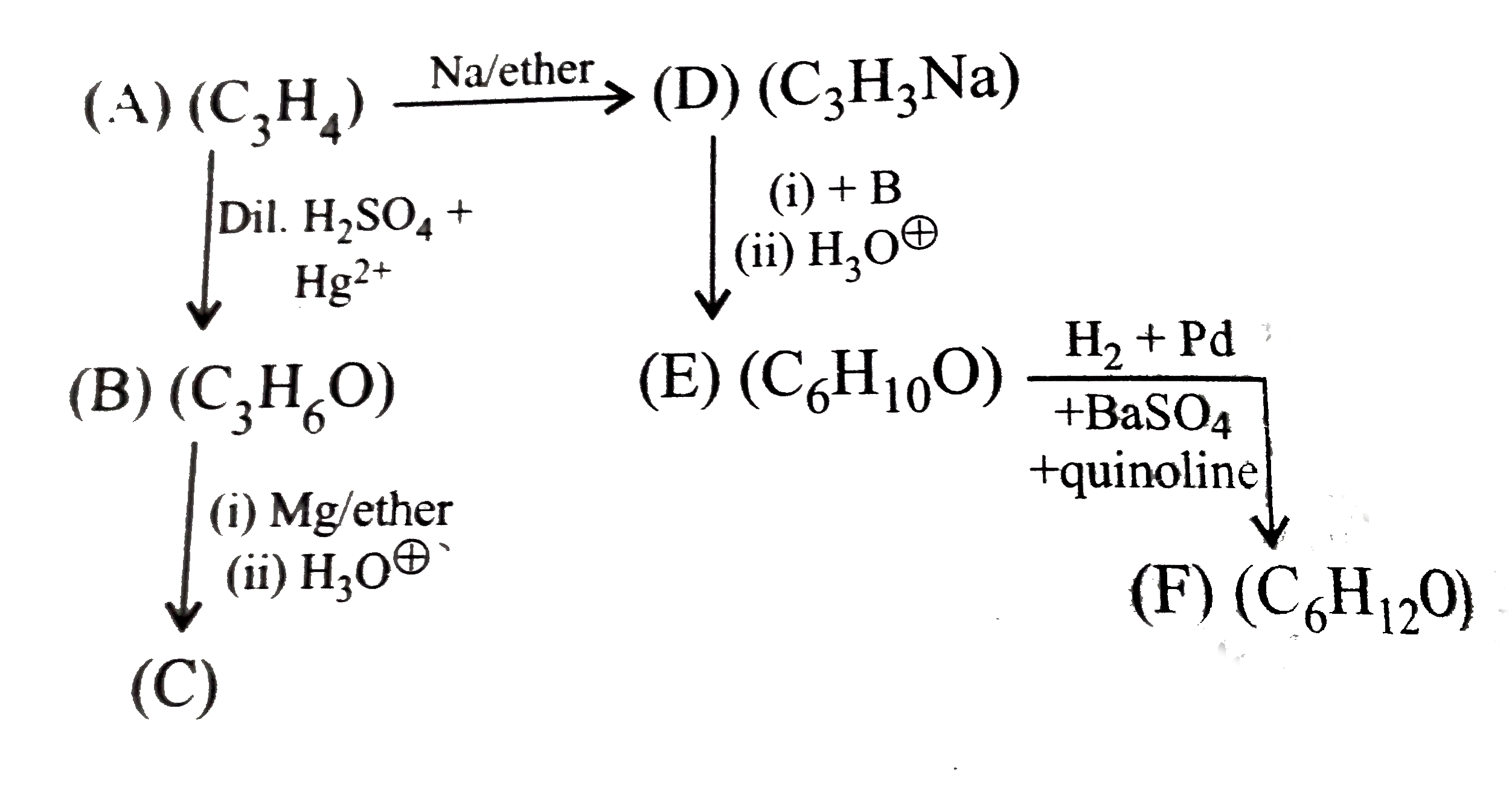
Which statement is correct for the formation of (B) form (A) ?View SolutionWrite down all the subsets of the following sets (i) {a} (ii) {a,b} (iii) {1,2,3} (iv) φ
View Solution

