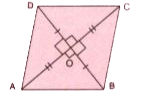
Which of the following statements are true for a rhombus? It has two pairs of parallel sides. It has two pairs of equal sides. It has only two pairs of equal sides. Two of its angles are at right angles. It diagonals bisect each other at right angles. Its diagonals are equal and perpendicular. It has all its sides of equal lengths. It is a parallelogram. It is a quadrilateral. It can be a square. It is a square.
To determine which statements about a rhombus are true or false, we will analyze each statement step by step.
1. It has two pairs of parallel sides.
- A rhombus is defined as a quadrilateral with opposite sides that are parallel. Therefore, this statement is True.
2. It has two pairs of equal sides.
- In a rhombus, all four sides are equal in length. Since having two pairs of equal sides implies that there are at least four equal sides, this statement is also True.
3. It has only two pairs of equal sides.
- Since a rhombus has all four sides equal, the statement that it has "only two pairs of equal sides" is misleading. This statement is False.
4. Two of its angles are at right angles.
- A rhombus does not necessarily have to have right angles. It can have angles that are not right angles. Therefore, this statement is False.
5. Its diagonals bisect each other at right angles.
- The diagonals of a rhombus do bisect each other and intersect at right angles. Thus, this statement is True.
6. Its diagonals are equal and perpendicular.
- While the diagonals of a rhombus are perpendicular, they are not necessarily equal. Therefore, this statement is False.
7. It has all its sides of equal lengths.
- By definition, all sides of a rhombus are equal in length. Hence, this statement is True.
8. It is a parallelogram.
- A rhombus is a specific type of parallelogram where all sides are equal. Thus, this statement is True.
9. It is a quadrilateral.
- A rhombus has four sides, making it a quadrilateral. Therefore, this statement is True.
10. It can be a square.
- A rhombus can be a square if all its angles are right angles. Thus, this statement is True.
11. It is a square.
- Not all rhombuses are squares. A rhombus only becomes a square when all angles are right angles. Therefore, this statement is False.
Summary of Statements:
1. True
2. True
3. False
4. False
5. True
6. False
7. True
8. True
9. True
10. True
11. False
- A rhombus is defined as a quadrilateral with opposite sides that are parallel. Therefore, this statement is True.
- In a rhombus, all four sides are equal in length. Since having two pairs of equal sides implies that there are at least four equal sides, this statement is also True.
- Since a rhombus has all four sides equal, the statement that it has "only two pairs of equal sides" is misleading. This statement is False.
- A rhombus does not necessarily have to have right angles. It can have angles that are not right angles. Therefore, this statement is False.
- The diagonals of a rhombus do bisect each other and intersect at right angles. Thus, this statement is True.
- While the diagonals of a rhombus are perpendicular, they are not necessarily equal. Therefore, this statement is False.
- By definition, all sides of a rhombus are equal in length. Hence, this statement is True.
- A rhombus is a specific type of parallelogram where all sides are equal. Thus, this statement is True.
- A rhombus has four sides, making it a quadrilateral. Therefore, this statement is True.
- A rhombus can be a square if all its angles are right angles. Thus, this statement is True.
- Not all rhombuses are squares. A rhombus only becomes a square when all angles are right angles. Therefore, this statement is False.
1. True
2. True
3. False
4. False
5. True
6. False
7. True
8. True
9. True
10. True
11. False
Topper's Solved these Questions
Similar Questions
Show that the diagonals of a square are equal and bisect each other at right angles.
View SolutionShow that the diagonals of a square are equal and bisect each other at right angles.
View SolutionShow that the diagonals of a square are equal and bisect each other at right angles.
View SolutionWhich of the following statements are true for a rectangle? It has two pairs of equal sides. It has all its sides of equal length. Its diagonals are equal. Its diagonals bisect each other. Its diagonals are perpendicular. Its diagonals are perpendicular and bisect each other. Its diagonals are equal and bisect each other. Its diagonals are equal and perpendicular, and bisect each other. All rectangles are squares. All rhombuses are parallelograms. All squares are rhombuses and also rectangles. All squares are not parallelograms.
View SolutionWhich of the following statements are true for a square? It is a rectangle. It has all its sides of equal length. Its diagonals bisect each other at right angle. Its diagonals are equal to its sides.
View SolutionState True or False
If the diagonals of a quadrilateral bisect each other at right angle, the quadrilateral is a square.
View SolutionIf the diagonals of a quadrilateral bisect each other at right angle, prove that the quadrilateral is a rhombus.
A rhombus has all its four sides equal.
View SolutionWhich of the following statements are true (T) and which are false (F)? (i) In a parallelogram, the diagonals are equal. (ii) In a parallelogram, the diagonals bisect each other. (iii) In a parallelogram, the diagonals intersect each other at right angles. (iv) In any quadrilateral, if a pair of opposite sides is equal, it is a parallelogram. (v) If all the angles of a quadrilateral are equal, it is a parallelogram. (vi) If three sides of a quadrilateral are equal , it is a parallelogram. (vii) If three angles of a quadrilateral are equal, it is a parallelogram. (viii) If all the sides of a quadrilateral are equal it is a parallelogram
View SolutionShow that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square
View SolutionShow that if the diagonals of a quadrilateral are equal and bisect each other at right angle, then it is a square.
View Solution
