Question

Show
that the diagonals of a square are equal and bisect each other at right
angles.

Explanation

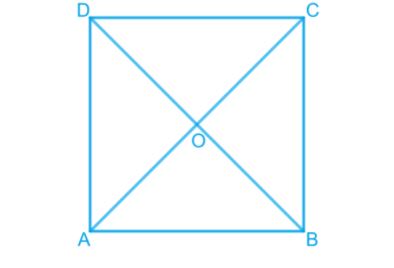
Given: The quadrilateral is a square.


To prove: Diagonals of a square are equal and bisect each other at right angles.


Thus, we have to prove` AC = BD, OA = OC, OB = OD`, and `∠AOB = 90^@`


Let` ABCD `be a square.


Let the diagonals `AC `and `BD` intersect each other at a point `O`.



In `ΔABC` and `ΔDCB`,


`AB = DC` (Sides of a square are equal to each other)


`∠ABC = ∠DCB` (All interior angles are of 90^@)


`BC = CB` (Common side)


`∴ ΔABC ≅ ΔDCB` (By SAS congruence rule)


`∴ AC = DB` (By CPCT) ------------ (1)


Hence, the diagonals of a square are equal in length.


In `ΔAOB` and `ΔCOD`,


`∠AOB = ∠COD` (Vertically opposite angles)


`∠ABO = ∠CDO` (Alternate interior angles)


`AB = CD` (Sides of a square are always equal)


`∴ ΔAOB ≅ ΔCOD` (By AAS congruence rule)


`∴ AO = CO` and `OB = OD` (By CPCT) ------------ (2)


Hence, the diagonals of a square bisect each other.


In `ΔAOB` and `ΔCOB`,


As we had proved that diagonals bisect each other,


Therefore, `AO = CO`


`AB = CB` (Sides of a square are equal)


`BO = BO` (Common)


`∴ ΔAOB ≅ ΔCOB` (By SSS congruency)


`∴ ∠AOB = ∠COB` (By CPCT) --------- (3)


However, `∠AOB + ∠COB = 180^@` (Linear pair)


`2∠AOB = 180^@` [From equation (3)]


`∠AOB = 90^@` ------------- (4)


Hence, from equation (1), (2) and (4), we see that the diagonals of a square are equal and bisect each other at right angles