Which one of the following points lies inside a circle of radius 6 and centre at (3,5) ?
(−2,−1)
(0,1)
(−1,−2)
(2,−1)
The correct Answer is:B
Radius of circle =6, centre =(3,5)
∴ Equation of circle is S≡(x−3)2+(y−5)2=(6)2
⇒≡(x−3)2+(y−5)2−36
Now, consider all the four options.
(a) (−2,−1)
Put it in S
S≡(−2,−3)2+(−1−5)2−36=25+36−36=25>0
⇒(−2,−1) is outside the circle.
(b) (0,1)
S≡(0−3)2+(1−5)2−36
=9+16−36=25−36=−11<0
Hence (0,1) lies inside a circle.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The centre of the circle is at the origin and its radius is 10. Which of the following points lies inside the circle?
A(6,8)B(0, 11)C(-10,0)D(7,7)A circle of radius 2 units is touching both the axes and a circle with centre at (6,5). The distance between their centres is
A8 unitsB5 unitsC7 unitsDnone of these
If d is the distance from a point P to the center of the circle of radius r and d−r>0, then the point P lies………… the circle. (outside/inside/on)
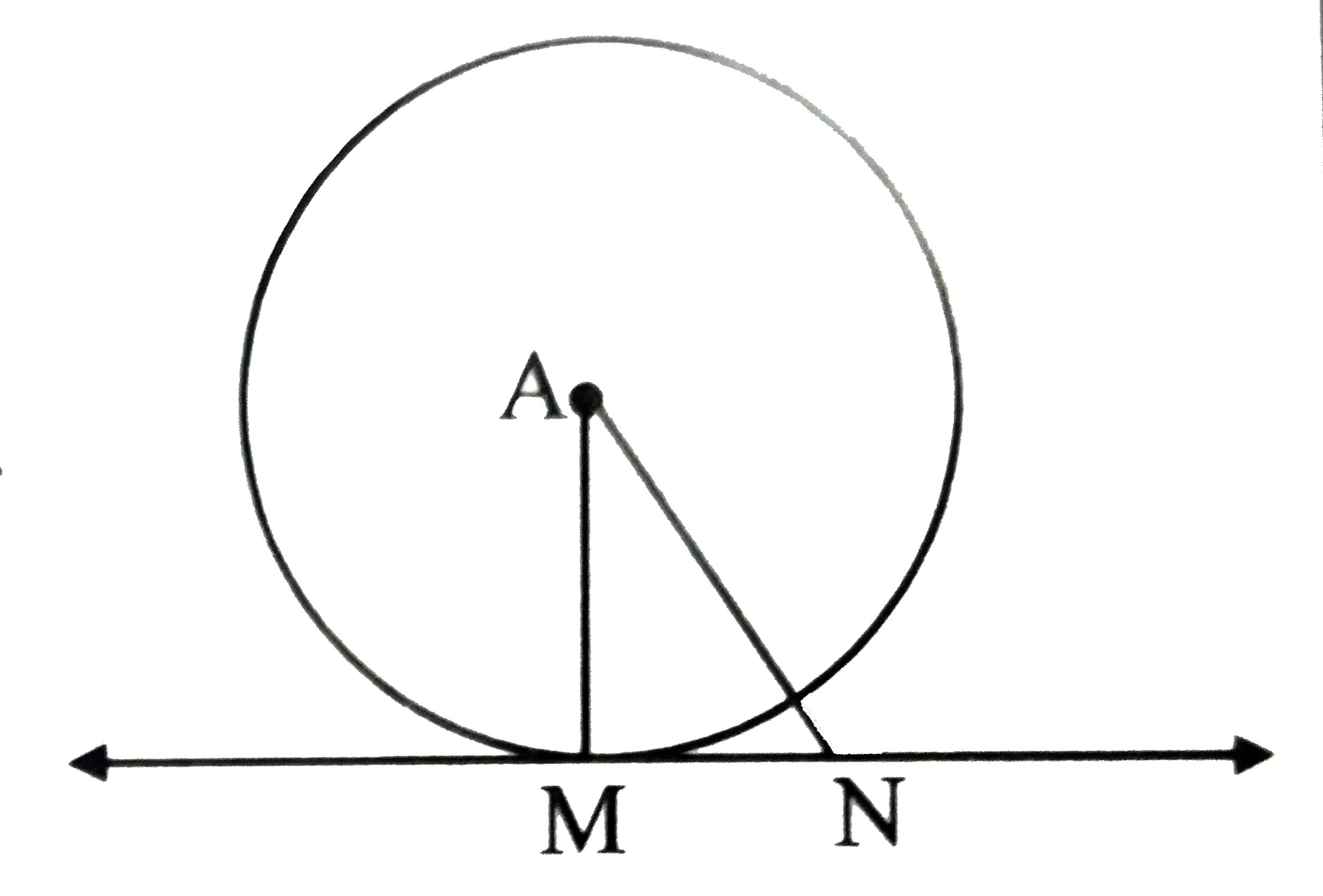
View SolutionIn the following figure, point ‘A’ is the centre of the circle. Line MN is tangent at point M. If AN = 12 cm and MN = 6 cm, determine the radius of the circle.

View SolutionLet C1 be the circle of radius r>0 with centre at (0,0) and let C2 be the circle of radius r with centre at (r,0) .The length of the arc of the circle C1 that lies inside the circle C2 ,is
View SolutionIn the following figure ,Point A is the centre of the circle . Line MN is tangent at point M. IF AN=12cm and MN=6cm , determine the radius of the circle.
View SolutionA line segment AB is the diameter of a circle with centre at O having radius 6.5 cm. Point P is in the plane of the circle such that AP=x and BP = y, In which one of the following cases the point P does not lie on the circle ?
View SolutionOne circle has a radius of 5 and its centre at (0,5). A second circle has a radius of 12and its centre at (12,0). What is the length of a radius of a third circle which passes through the centre of the second circle and both the points of intersection of the first two circles.
View Solution
