Which point maximise the objective function P=x4+9y20?
(0,0)
(0,150)
-90150
(160,0)
The correct Answer is:C
Topper's Solved these Questions
Similar Questions
Knowledge Check
To maximise the objective function z=x+2y under the constraints x−y≤2,x+y≤4andx,y≥0 is
A1x=0,y=4,z=8Bx=1,y=2,z=5Cx=1,y=4,z=9Dx=0,y=3,z=6The vertices of a closed convex polygon representing the feasible region of the objective function are (6,2),(4,6),(5,4) and (3,6). Find the maximum value of the function f=7x+11y
A61B69C59D49If the corner points of the feasible region for an L.P.P. are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5), then the minimum value of the objective function F=4x+6y occurs at
AA) (0, 2) onlyBB) (3, 0) onlyCC) the mid-point of the line segment joining the point (0, 2) and (3, 0) onlyDD) every point on the line segment joining the point (0, 2) and (3, 0)
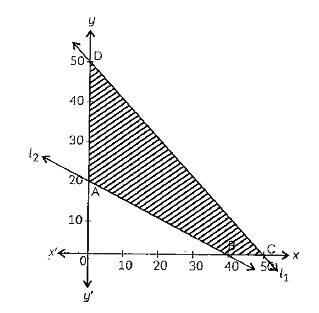
The feasible region of a system of linear inequalities is shown below. If the objective function is maximise Z = 25x + 15y, then the maximum value of Z occurs at:
View SolutionShow that the minimum of Z occurs at more than two points : Maximise Z=x+y, subject to x−y≤−1,−x+y≤0,x,y≥0.
View SolutionSolve the following L.P.P graphically
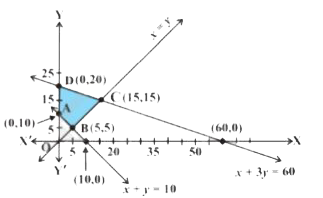
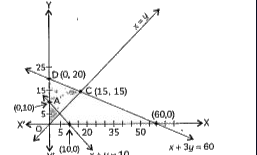
Minimise and maximise z = 3x + 9y
Subject to the constraints x+3y≤60
x+y≥10
x≤y
x≥0,y≥0
View SolutionIf the objective function for an L.P.P. is Z=3x+4y and the corner points for unbounded feasible region are (9, 0), (4, 3), (2, 5), and (0, 8), then the maximum value of Z occurs at
View SolutionThe corner points of the feasible region are (800 , 400) , (1050,150) , (600,0) . The objective function is P=12x+6y. The maximum value of P is
View Solution